Методы обнаружения мультиколлинеарности

Признаки наличия мультиколлинеарности:

1) коэффициент детерминации R² достаточно высок, но все или некоторые коэффициенты уравнения регрессии статистически не значимы (низкие t-статистики);

2) высокие парные коэффициенты корреляции.

Для проверки этого признака формируется определитель матрицы парных коэффициентов между объясняющими переменными

R = , (4.21)

где 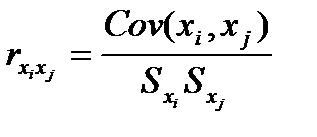. (4.22)

Матрица R – симметричная, причем на главной диагонали стоят единицы, т.е. =1. При полном отсутствии корреляции между факторами =0, при , и определитель R равен 1. Если же между факторами существует полная линейная зависимость, т.е. =1, то det R = 0.

Таким образом, чем ближе к нулю det R, тем сильнее мультиколлинеарность. Вывод о наличии мультиколлинеарности делается по результатам проверки нулевой гипотезы Н₀ : det R = 1, при альтернативной гипотезе Н₁ : det R = 0.

Статистическая проверка гипотез:

Н₀ : det R = 1;

Н₁ : det R = 0

осуществляется с помощью - распределения.

Величина

(4.23)

сравнивается с критическим значением ( ), где n – объем выборки, m – количество объясняющих переменных.

Если > , то Н₀ отклоняется и делается вывод о наличии мультиколлинеарности;

3) высокие частные коэффициенты корреляции.

Частные коэффициенты корреляции – это коэффициенты корреляции между двумя факторами, «очищенные» от влияния других факторов. Например для трех факторов Х₁, Х₂, Х₃ частный коэффициент корреляции для Х₁, Х₂ будет

, (4.24)

где – парный коэффициент корреляции между Х₁ и Х₂ ; – частный коэффициент корреляции между Х₁ и Х₂.

Схема вычисления элементов матрицы частных коэффициентов корреляции:

а) обращение матрицы парных коэффициентов корреляции (4.21)

R^-1 = C = ; (4.25)

б) вычисление частных коэффициентов корреляции

. (4.26)

Частные коэффициенты корреляции могут быть использованы для определения «чистого» влияния Х_j на Y и ранжирования таким образом зависимости Х_j на результат. Для этого составляется расширенная матрица частных коэффициентов:

	Y	X1	X2	…	Xm
Y				…
X1				…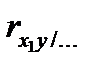
X2				…
…	…	…	…	…	…
Xm				…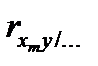

Частные коэффициенты корреляции определяют степень линейной зависимости Х_j и Y.