
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Методические советы по выполнению контрольной работы 2 страница
Так как, правило сложения дисперсий соблюдается, то по максимальной величине частной дисперсии  можно считать, что наиболее эффективной системой оплаты труда по исследуемой совокупности является сдельная прогрессивная оплата труда.
можно считать, что наиболее эффективной системой оплаты труда по исследуемой совокупности является сдельная прогрессивная оплата труда.
Задача 10 представлена по теме «Выборочное наблюдение».
Пример решения задачи 10.Для определения расчетов с кредиторами предприятий корпорации в коммерческом банке была проведена случайная выборка 100 платежных документов, по которым средний срок перечисления и получения денег оказался равным 22 дням  со стандартным отклонением 6 дней
со стандартным отклонением 6 дней  .
.
Необходимо с вероятностью  определить предельную ошибку выборочной средней и доверительные пределы средней продолжительности расчетов предприятий данной корпорации.
определить предельную ошибку выборочной средней и доверительные пределы средней продолжительности расчетов предприятий данной корпорации.
Для вероятности  находим
находим 
Предельную ошибку определим по формуле повторного отбора, так как численность генеральной совокупности  неизвестна:
неизвестна:
 (11)
(11)

Предельную относительную ошибку выборки рассчитаем по формуле:
 (12)
(12)

Генеральная средняя будет равна  , а доверительные интервалы (пределы) генеральной средней рассчитаем по формуле исходя из двойного неравенства:
, а доверительные интервалы (пределы) генеральной средней рассчитаем по формуле исходя из двойного неравенства:
 (13)
(13)
Тогда 

Таким образом, с вероятностью 0,954 можно утверждать, что средняя продолжительность расчетов предприятий данной корпорации колеблется в пределах от 20,8 до 23,2 дня.
Задача 11 составлена по теме «Статистическое изучение динамики. Показатели анализа ряда динамики».
Пример решения задачи.Имеются данные о числе родившихся в Чувашской Республике за 2005-2010 гг., чел. (табл. 14).
Таблица 14 – Число родившихся
| 2005 г. | 2006 г. | 2007 г. | 2008 г. | 2009 г. | 2010 г. |
Определите аналитические показатели ряда динамики числа родившихся в Чувашской Республике за 2005 – 2010 гг.: 1) абсолютные приросты; 2) темпы роста; 3) темпы прироста; 4) абсолютное значение одного процента прироста, а также средние показатели (средний уровень ряда и средние показатели изменения уровней ряда). Сделайте прогноз на три предстоящих года по среднему абсолютному приросту и среднему темпу роста. Постройте график.
В зависимости от задачи исследования абсолютные приросты  , темпы роста
, темпы роста  и темпы прироста
и темпы прироста  могут быть исчислены с использованием постоянной базы сравнения (базисные) и переменной базы сравнения (цепные).
могут быть исчислены с использованием постоянной базы сравнения (базисные) и переменной базы сравнения (цепные).
1. Абсолютный прирост  - разность между последующим уровнем ряда и базисным (или предыдущим).
- разность между последующим уровнем ряда и базисным (или предыдущим).
Абсолютный прирост базисный рассчитывается по формуле:
 (14)
(14)
Так, 
 и т.д.
и т.д.
Абсолютный прирост цепной рассчитывается по формуле:
 (15)
(15)
Так, 
 и т.д.
и т.д.
Таблица 15 - Динамика числа родившихся в Чувашской Республике
| Годы | Число родившихся, чел. | Абсолютный прирост, чел. | Темпы роста, % | Темпы прироста, % | Абсолютное значение 1 % прироста, чел. | |||
| базисный | цепной | базисный | цепной | базисный | цепной | |||
| А | ||||||||
| - | - | - | - | - | - | |||
| 101,20 | 101,20 | 1,20 | 1,20 | 131,33 | ||||
| 112,96 | 111,62 | 12,96 | 11,62 | 132,91 | ||||
| 113,97 | 100,89 | 13,97 | 0,89 | 148,35 | ||||
| 122,62 | 107,59 | 22,62 | 7,59 | 149,67 | ||||
| 123,16 | 100,44 | 23,16 | 0,44 | 161,03 |
Следует отметить, что сумма цепных абсолютных приростов равна последнему базисному абсолютному приросту.
2. Темп роста  - отношение уровней ряда динамики, которое выражается в коэффициентах и процентах.
- отношение уровней ряда динамики, которое выражается в коэффициентах и процентах.
Темп роста базисный определяется отношением каждого последующего уровня к базисному значению по формуле:
 (16)
(16)
Так, 
 и т.д.
и т.д.
Темп роста цепной определяется отношением последующего уровня к предыдущему по формуле:
 (17)
(17)
Так, 
 и т.д.
и т.д.
Между цепными и базисными темпами роста имеется взаимосвязь: произведение соответствующих цепных темпов роста равно базисному. Зная базисные темпы, можно исчислить цепные делением каждого последующего базисного темпа роста на каждый предыдущий.
3. Темп прироста  определяют двумя способами:
определяют двумя способами:
а) темп прироста базисный - отношение абсолютного прироста базисного к базисному значению:
 (18)
(18)
Так, 
 и т.д.
и т.д.
Темп прироста цепной - отношение абсолютного прироста цепного к цепному значению:
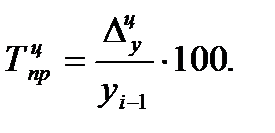 (19)
(19)
Так, 
 и т.д.
и т.д.
б) как разность между коэффициентом роста и единицей, если темпы роста выражены в коэффициентах:
 (20)
(20)
или как разность между темпами роста и 100 %, еслитемпы роста выражены в процентах:
 (21)
(21)
Так, 
 и т.д.
и т.д.

 и т.д.
и т.д.
4. Абсолютное значение одного процента прироста  так же исчисляют двумя путями:
так же исчисляют двумя путями:
а) отношение абсолютного прироста цепного к темпу прироста цепного:
 (22)
(22)
Так, 
 и т.д.
и т.д.
б) как одна сотая часть предыдущего уровня:
 (23)
(23)
Так, 
 и т.д.
и т.д.
Средний уровень ряда рассчитаем по формуле:
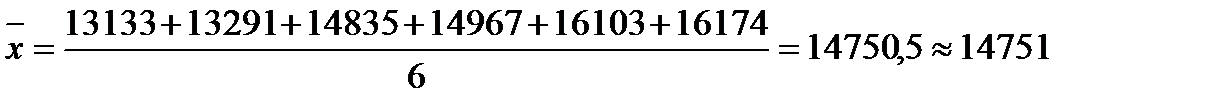 чел.
чел.
Средний абсолютный прирост исчисляется двумя способами:
а) как средняя арифметическая простая годовых абсолютных (цепных) приростов

б) как отношение базисного абсолютного прироста к числу периодов

Средний темп роста исчисляется двумя способами:
а) как средняя геометрическая цепных коэффициентов роста по «цепному» способу


б) по «базисному» способу

Средний темп прироста определим по формуле:
 (24)
(24)
или средний коэффициент роста:
 (25)
(25)
Так, 
Таким образом, ежегодно в Чувашской Республике увеличилось число родившихся на 608 человек, или на 4,25 %.
Составим прогноз числа родившихся в Чувашской Республике на предстоящие три года по среднему абсолютному приросту по формуле:



По среднему темпу роста прогнозные показатели определим по формуле: 


Более наглядно этот прогноз изобразим на графике (рис. 1).
Рис. 1. Динамика и прогноз числа родившихся в Чувашской Республике
Таким образом, по нашим прогнозам в Чувашии будет наблюдаться рост рождаемости.
Задачи 12…14 составлены по теме «Методы анализа основных тенденций развития в рядах динамики, экстраполяция и прогнозирование».
Пример решения задачи 12.По данным табл. 16 выявите основную тенденцию методами скользящей (подвижной) средней и аналитического выравнивания по прямой. Результат экстраполяции прогноза добычи газа представьте в виде точечных оценок и определите вероятностные границы интервала. Постройте графики. Сделайте выводы.
Таблица 16 –Добыча естественного газа в Российской Федерации, млн. м3
| Год | Добыча естественного газа, млн. м3 | Год | Добыча естественного газа, млн. м3 |
Источник. Регионы России. Социально – экономические показатели. – 2003, 2009.
Расчет скользящей средней по данным добычи естественного газа приведен в табл. 17.
Таблица 17 – Исходные данные и результаты расчета скользящей средней
| Год | Добыча естественного газа, млн. м3 | Скользящая средняя | |
| трехлетняя | пятилетняя | ||

| |||

| 590208,4 | ||
| 587901,6 | |||
| 588991,3 | 583895,8 | ||
| 585672,3 | 588704,6 | ||
| 586827,3 | 594471,4 | ||
| 598927,7 | 602667,8 | ||
| 615987,7 | 614041,4 | ||
| 631219,3 | |||
| 643231,7 | 640533,8 | ||
| 649937,3 | |||
| 658178,7 | 639962,8 | ||
| 634247,3 | |||
Таким образом, скользящие средние выявляют основную тенденцию добычи газа в РФ. Снижение производства газа в 2009 г. по всей видимости вызвано кризисом 2008-2009 гг.
Рис. 2. Добыча естественного газа в Российской Федерации
Рассмотрим метод аналитического выравнивания ряда динамики по прямой  . Определим параметры
. Определим параметры  и
и  методом наименьших квадратов, решив систему нормальных уравнений:
методом наименьших квадратов, решив систему нормальных уравнений:
 (26)
(26)
где  - фактические уровни ряда,
- фактические уровни ряда,
 - время (порядковый номер периода или момента времени).
- время (порядковый номер периода или момента времени).
Упростим расчет параметров, взяв за начало отсчета времени (t=0) центральный интервал (момент).
Так как у нас для расчетов было взято 15 лет (нечетное число), то обозначим время t, используя ноль (табл. 18).
Таблица 18 - Расчетные данные для определения параметров системы нормальных уравнений и выровненных теоретических значений (  )
)
| Годы | Добыча естественного газа, млн. м3 | t | t 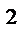
| yt | 
| ||||
| -7 | -4168269 | 540508,4 | |||||||
| -6 | -3608832 | 545004,5 | |||||||
| -5 | -2855310 | 549500,6 | |||||||
| -4 | -2365600 | 553996,7 | |||||||
| -3 | -1774923 | 558492,8 | |||||||
| -2 | -1167866 | ||||||||
| -1 | -581443 | 567485,1 | |||||||
| 571981,2 | |||||||||
| 576477,3 | |||||||||
| 580973,4 | |||||||||
| 585469,6 | |||||||||
| 589965,7 | |||||||||
| 594461,8 | |||||||||
| 598957,9 | |||||||||
| Итого | |||||||||
Так как  , то система нормальных уравнений примет вид:
, то система нормальных уравнений примет вид:
 (27)
(27)
Тогда из первого и второго уравнений поочередно получим  и
и 
Получим уравнение прямой 
Теперь подставив поочередно значения t из таблицы 3 в полученное уравнение, заполним последний столбец этой же таблицы (рис. 3).
 , то есть задачу мы решили верно.
, то есть задачу мы решили верно.
Рис. 3. Прогноз добычи полезных ископаемых
Теперь получим точечный прогноз, подставив в это уравнение значение t по возрастанию, так
 млн. м3;
млн. м3;
 млн. м3;
млн. м3;
 млн. м3.
млн. м3.
Параметры  и
и  можно вычислить иначе с помощью определителей по формулам:
можно вычислить иначе с помощью определителей по формулам:
 (28)
(28)
 (29)
(29)
Вспомогательные расчеты проведем в таблице 19, взяв величину t в порядке возрастания.
Таблица 19 – Расчет параметров  и
и  с помощью определителей
с помощью определителей
| Годы | Добыча естественного газа, млн. м3 | t | t 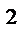
| yt | 
|
| 444808,4 | |||||
| 466003,9 | |||||
| 487199,3 | |||||
| 508394,8 | |||||
| 529590,3 | |||||
| 550785,7 | |||||
| 571981,2 | |||||
| 593176,6 | |||||
| 614372,1 | |||||
| 635567,6 | |||||
| 677958,5 | |||||
| 699153,9 | |||||
| 720349,4 | |||||
| Итого |
Подставим расчетные данные в формулы:
 млн. м3;
млн. м3;
 млн. м3.
млн. м3.
Отсюда получим линейное уравнение:

Параметры уравнения парной линейной регрессии можно рассчитать и по следующим формулам:
 (30)
(30)
 (31)
(31)
Подставив значения t по возрастанию, получим прогноз показателя на три года:
 млн. м3;
млн. м3;
 млн. м3;
млн. м3;
 млн. м3.
млн. м3.
Более наглядно изобразим на рис. 13.
Рассчитаем экстраполируемые прогнозные значения в виде интервальной оценки. Для этого воспользуемся формулой:
 , (32)
, (32)
то есть
 (33)
(33)
где  - коэффициент доверия по критерию Стьюдента;
- коэффициент доверия по критерию Стьюдента;
 - остаточное среднее квадратическое отклонение от тренда.
- остаточное среднее квадратическое отклонение от тренда.
Рис. 4. Прогноз добычи полезных ископаемых
В таблице 20 приведем необходимые расчеты.
Таблица 20 – Вспомогательная таблица
| Годы | Добыча естественного газа, млн. м3 
| 
| 
| 
|
| 444808,4 | 156663,6 | |||
| 466003,9 | 105058,1 | |||
| 487199,3 | 104200,7 | |||
| 508394,8 | 83246,2 | |||
| 529590,3 | 54342,7 | |||
| 550785,7 | 30657,3 | 939870043,3 | ||
| 571981,2 | 23124,8 | |||
| 593176,6 | 27057,4 | 732102894,8 | ||
| 614372,1 | 18250,9 | 333095350,8 | ||
| 635567,6 | 5233,4 | 27388475,56 | ||
| -492 | ||||
| 677958,5 | -25218,5 | 635972742,3 | ||
| 699153,9 | -33628,9 | |||
| 720349,4 | -135872,4 | |||
| Итого | - | - | 108650969937,47 |
Остаточное среднее квадратическое отклонение от тренда рассчитаем по формуле:

где  - число уровней ряда динамики;
- число уровней ряда динамики;
 - число параметров адекватной модели тренда.
- число параметров адекватной модели тренда.
Согласно таблице Стьюдента (приложение 2) при уровне значимости  коэффициент доверия составляет 2,1604.
коэффициент доверия составляет 2,1604.
Согласно точечной оценке прогнозного значения добыча естественного газа в 2010 г. составит 607950,16 млн. м3. Тогда вероятностные границы интервала будут в пределах


Вероятностные границы на 2011 г. и 2012 г. рассчитайте самостоятельно.
Пример решения задачи 13. По данным табл. 21 выявите основную тенденцию методом аналитического выравнивания по прямой по формулам и с помощью статистическо функции ЛИНЕЙН, а экспоненциальный тренд рассчитайте, используя функцию ЛГРФПРИБЛ.
Согласно условию задачи число уровней четное число равное 6, поэтому условное обозначение времени будет как бы в полугодиях.
Таблица 21 - Расчетные данные для определения параметров системы нормальных уравнений и выровненных теоретических значений (  )
)
| Годы | Посевные площади всех сельскохозяйственных культур, тыс. га | t | t 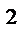
| yt | 
|
| 551,3 | -5 | -2757 | 546,03 | ||
| 549,1 | -3 | -1647 | 553,59 | ||
| 549,9 | -1 | -549,9 | 561,15 | ||
| 571,7 | +1 | 571,7 | 568,71 | ||
| 595,7 | +3 | 1787,1 | 576,27 | ||
| 571,9 | +5 | 2859,5 | 583,83 | ||
| Итого | 3389,6 | 264,6 | 3389,6 | ||
| +7 | 591,39 | ||||
| +9 | 598,95 | ||||
| +11 | 606,51 |
Источник. Сельское хозяйство, охота и охотное хозяйство, лесоводство в России. 2011. Стат. сб. /Росстат – М., 2011. –С. 220.
Дата добавления: 2014-12-23; просмотров: 334; Мы поможем в написании вашей работы!; Нарушение авторских прав |