Методические советы по выполнению контрольной работы 5 страница

Получаем уравнение регрессии:

Решим эту задачу с помощью программы Statgraphics (рис. 29).

Тесноту связи определим, рассчитав индекс корреляции:

Коэффициент детерминации составил 0,5075, таким образом, на 50,75% вариации объясняется вариацией , на долю прочих факторов приходится 49,25 %.

Рассчитаем F-критерий Фишера по формуле:

Рис. 29. Результаты расчетов

Таким образом, мы получили те же значения. Небольшие различия объясняются округлением.

Табличное значение F-критерий Фишера составило 4,41. Так как фактическое значение F превышает табличное, уравнение регрессии статистически значимо.

Определим среднюю ошибку апроксимации по формуле:

Этот показатель не выше 8 - 10 %, т.е. среднее отклонение расчетных и фактических данных не столь велико.

е) рассмотрим обратную функцию:

. (42)

Для оценки параметров приведем уравнение к линейному виду при . Затем получим

Воспользуемся методом наименьших квадратов и получим систему уравнений:

Таблица 28 - Данные для уравнения связи и коэффициента корреляции

№ хозяйства
	0,0578035		2,3121387		19,2678227	3,8723263	11,3747
	0,0558659		2,3463687		19,4174757	2,3027326	8,477518
	0,0471698		2,1226415		19,6463654	2,4137804	7,328465
	0,0487805		2,3414634		19,8807157	0,383513	3,020899
	0,0471698		2,2641509		19,8807157	1,740511	6,223039
	0,0537634		3,2795699		20,9643606	5,590201	12,71162
	0,0512821		3,3333333		21,3219616	3,3195441	9,343393
	0,0505051		3,3333333		21,4132762	2,6026602	8,14786
	0,0416667		3,0833333		22,172949	3,3381153	7,612712
	0,0471698		3,5377358		22,2717149	1,1485729	5,055259
	0,0512821		4,0512821		22,675737	10,085305	16,28583
	0,0357143				23,2018561	23,022184	17,13623
	0,0444444		3,7777778		23,3100233	0,6561378	3,600104
	0,0416667		3,5833333		23,4192037	0,3373243	2,419984
	0,0408163		3,5510204		23,5294118	0,9420415	3,961585
	0,0444444		4,2222222		24,4498778	3,8020232	8,666123
	0,0411523		4,1152263		25,0626566	0,5816452	3,138505
	0,0327869		3,2786885		25,0626566	29,564703	17,82736
	0,0350877		3,5087719		25,0626566	11,815329	12,06085
	0,0337838		3,3783784		25,0626566	20,587485	15,32886
Итого	0,9023554		64,42077		447,074094	128,10614	179,7209

Получим систему нормальных уравнений:

Получаем уравнение регрессии:

Решим эту задачу с помощью программы Statgraphics (рис. 30).

Таким образом, мы получили те же значения. Небольшие различия объясняются округлением.

Тесноту связи определим, рассчитав индекс корреляции:

Коэффициент детерминации составил 0,5565, таким образом, на 55,65% вариации объясняется вариацией , на долю прочих факторов приходится 44,35 %.

Рассчитаем F-критерий Фишера по формуле:

Рис. 30. Результаты расчетов

Табличное значение F-критерий Фишера составило 4,41. Так как фактическое значение F превышает табличное, уравнение регрессии статистически значимо.

Определим среднюю ошибку апроксимации по формуле:

Этот показатель не выше 8 - 10 %, т.е. среднее отклонение расчетных и фактических данных не столь велико.

ж) рассмотрим функцию:

. (43)

Воспользуемся программой Statgraphics (рис. 31) и получим уравнение регрессии: .

Таблица 29 - Данные для расчета коэффициентов

№ хозяйства
	17,3		17,309697	9,40261E-05	0,056050315
	17,9		17,70052	0,039792138	1,114411557
	21,2		18,271088	8,578526578	13,81562351
	20,5		18,824369	2,807738202	8,173808233
	21,2		18,824369	5,643621165	11,20580513
	18,6		21,054577	6,02494794	13,1966502
	19,5		21,694719	4,81679326	11,2549713
	19,8		21,851825	4,209986222	10,36275301
			23,070187	0,86455174	3,874219769
	21,2		23,217988	4,072274111	9,518809617
	19,5		23,800012	18,4901066	22,05134562
			24,508114	12,19326952	12,47102229
	22,5		24,647293	4,610867034	9,543524244
			24,785691	0,617309766	3,273710958
	24,5		24,92332	0,179199656	1,72783593
	22,5		25,998137	12,2369655	15,54727748
	24,3		26,647893	5,512601421	9,662111008
	30,5		26,647893	14,83872853	12,6298591
	28,5		26,647893	3,430300433	6,498621141
	29,6		26,647893	8,714935888	9,973334544
Итого	455,1		457,07348	117,8826097	185,9517449

Решим эту задачу с помощью программы Statgraphics (рис. 31):

Рис. 31. Результаты расчетов

Тесноту связи определим, рассчитав индекс корреляции:

Коэффициент детерминации составил 0,5919, таким образом, на 59,19% вариации объясняется вариацией , на долю прочих факторов приходится 40,81 %.

Рассчитаем F-критерий Фишера по формуле:

Табличное значение F-критерий Фишера составило 4,41. Так как фактическое значение F превышает табличное, уравнение регрессии статистически значимо.

Определим среднюю ошибку апроксимации по формуле:

Этот показатель не выше 8 - 10 %, т.е. среднее отклонение расчетных и фактических данных не столь велико.

Теперь необходимо определить наиболее точную модель, учитывая коэффициенты детерминации и апроксимации. Так, уравнение регрессии наиболее точно отражает исходные данные. Так как коэффициент детерминации наибольший, а коэффициент апроксимации наименьший.

Задача 18.Имеются данные об урожайности картофеля, количество внесенных удобрений и доле высокосортных посевов (табл. 30). Определите показатели связи при множественной линейной зависимости расчетным путем с помощью инструмента анализа данных Регрессияи программыStatgraphics.

Таблица 30 - Данные для уравнения связи и коэффициента множественной корреляции

Номер хозяйства	Исходные данные	Расчетные данные
урожайность картофеля, ц/га ( )	внесено органических удобрений, т/га ( )	удельный вес высокосортных посевов, %
Итого

Исследование формы зависимости между указанными признаками позволяет сделать вывод, что связь может быть выражена при помощи линейного уравнения

(44)

где - урожайность картофеля, ц/га;

- количество внесенных органических удобрений под картофель, т/га;

- удельный вес посевов высокосортными семенами, %.

Требуется определить параметры уравнения связи коэффициент множественной корреляции.

Решение:Составим систему нормальных уравнений с тремя неизвестными:

(45)

Подставив в эту систему данные из табл. 261, получим:

Разделим каждое из уравнений на коэффициенты при первом известном : первое уравнение - на 20, второе - на 354, третье - на 1508, получим:

Теперь поочередно вычтем первое уравнение из второго и третьего:

(175,2 - 164,5) = - + (19,0 - 17,7) + (79,5 - 75,4) ;

(173,3-164,5) = - + (18,6 – 17,7) + (78,9 – 75,4) .

Получим:

Разделив каждое из двух этих уравнений на коэффициент при , первое уравнение - на 1,3, второе - на 0,9, получим:

Из второго уравнения вычитаем первое и освобождаемся от параметра : 9,78 -8,23 = (3,8889 - 3,1538)а₂, 1,55 = 0,73 5а₂, отсюда а₂ = 1,55 : 0,735 = 2,11. Подставляем значение а₂ в уравнение 8,23 = + 3,1538 ∙ 2,11, отсюда = 1,58. Далее надо найти значение параметра а_о, для чего используем уравнение 164,5 = + 17,7 ∙ 1,58 + 75,4 ∙ 2,11. Сделаем соответствующие расчеты: 164,5 = + 27,966 + 159,09; отсюда а₀ .= - 22,6. Уравнение множественной линейной зависимости примет вид:

Параметры уравнения множественной регрессии показывают, что с увеличением дозы внесения органических удобрений на 1 т в расчете на 1 га урожайность картофеля возрастает на 1,58 ц, а повышение удельного веса высокосортных семян на 1 % дает прирост урожайности 2,11 ц. Параметр экономического смысла не имеет.

Теперь определим тесноту связи. Рассчитаем множественный (совокупный) коэффициент корреляции по формуле

(46)

Для его расчета надо найти средние значения , а также средние квадратические отклонения по урожайности, внесению удобрений и удельному весу высокосортных семян:

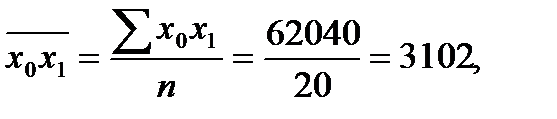
Теперь рассчитаем средние квадратические отклонения:

Рассчитаем парные коэффициенты корреляции:

Эти коэффициенты можно рассчитать с помощью MS Excel. В главном меню последовательно выбираем Данные /Анализ данных /Корреляция (рис. 32).

Рис. 32. Расчет коэффициентов корреляции

Так же можно воспользоваться программой Statgraphics, используя в расчетах функцию Multiple Variable Analisis (рис. 33).

Подставив значения коэффициента корреляции и детерминации в формулу множественной (совокупной) корреляции получим:

Связь между признаками очень тесная, так как коэффициент множественной корреляции составляет 0,981, а детерминации — 0,962. т.е. 96,2 % колебаний урожайности картофеля в данных условиях зависит от исследуемых факторов и только 3,8 % - от других, не уточненных в анализе.

Значимость 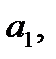оценим t-критерием Стьюдента:

Рис. 33. Расчет коэффициентов корреляции

Табличное значение t-критерия Стьюдента при 5 % уровне значимости и 17 степенях свободы (n-m=20-2-1=17) составляет 2,1098. Так как только при условии оба фактора 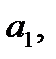, считаются значимыми. Однако меньше положенного. Поэтому величина является статистически незначимой, ненадежной, т.е. она сформировалась под воздействием случайных факторов. То же касается и величины .

Теперь воспользуемся инструментом анализа данных Регрессия (рис. 34).

Рис. 34. Результаты расчетов

Уравнение множественной линейной зависимости примет вид: . Коэффициент детерминации 0,9629.

Табличное значение F-критерий Фишера составило 3,59, расчетное – 220,59. Так как фактическое значение F превышает табличное, уравнение регрессии статистически значимо.

Решим эту же задачу с помощью программы Statgraphics, используя в расчетах функцию Multiple Regression (рис. 35).

Рис. 35. Результаты расчетов

Уравнение множественной линейной зависимости примет вид: . Случайные ошибки параметров , , равны , , . Эти значения указывают на величину, сформировавшуюся под воздействием случайных факторов. На их основе рассчитываются значения t-критерия Стьюдента: , , . На основе Приложения 2 определим критические значения t-критерия Стьюдента для уровня значимости , т.е. с вероятностью 0,95 составит 2,1098, , т.е. с вероятностью 0,99 – 2,8982. Статистически значимыми здесь являются , , а величина сформировалась под воздействием случайных причин.