Методические советы по выполнению контрольной работы 6 страница

Так как фактические значения больше теоретических (критических), то делаем вывод о существенности данных параметров ( и ), которые формируются под воздействием не случайных причин. Об это же свидетельствует показатель вероятности случайных значений параметров регрессии, так и То есть вероятность случайно получить такие значения t-критерия Стьюдента составляет 4,8 % и 0,0000, что не превышает допустимый уровень значимости 5 %.

Чуть ниже на рис. 44 представлен расчет F-критерий Фишера, и он составляет 29,23. Согласно дисперсионному анализу вероятность получить случайно такое значение F-критерий Фишера составляет 0,0000, что не превышает допустимый уровень значимости 5%.

Отсюда же берем нескорректированный коэффициент детерминации , который оценивает долю вариации результата в зависимости от факторов в общей вариации. Этот показатель показывает на достаточно высокую связь результата и от факторного признака. Скорректированный коэффициент детерминации оценивает тесноту связи с учетом степеней свободы общей и остаточной дисперсий. Он дает такую оценку тесноты связи, которая не зависит от числа факторов в модели и поэтому может сравниваться по разным моделям с разным числом факторов.

Табличное значение F-критерий Фишера составило 3,59, расчетное – 220,59. Так как фактическое значение F превышает табличное, уравнение регрессии статистически значимо.

Задача 19.Определение показателей связи при парной криволинейной зависимости.

Пример решения задачи 19. Имеются данные по группе коров об их продуктивности возрасте (числе отелов) (табл. 31).

Таблица 31- Данные для уравнения связи и индекса корреляции (корреляционное отношение)

№ п/п	Исходные данные	Расчетные данные
относительное изменение удоя, %, ( )	возраст коров к моменту отела, лет ( )
								80,649	198,16	154,45
		2,5	6,25	15,625	39,06		512,5	83,965	122,7	83,032
								86,979	36,929	37,185
		3,5	12,25	42,875	150,06			89,692	1,1598	11,459
								92,103	0,8521	0,9485
								96,021	24,237	8,6676
								98,733	47,929	31,991
								100,24	35,083	51,295
								100,54	35,083	55,683
								99,633	24,237	42,982
								97,521	8,5444	19,75
								94,203	0,8521	1,2681
								89,679	1,1598	11,546
Итого			667,5	6141,5	60898,125		63639,5		536,92	510,26

Анализ исходных данных позволил установить, что зависимость криволинейная и может быть описана уравнением параболы 2-го порядка:

(47)

Требуется определить параметры уравнения связи и индекс корреляции.

Решение:Составим систему уравнений для нахождения параметров , , :

В систему уравнений подставим данные из табл. 266:

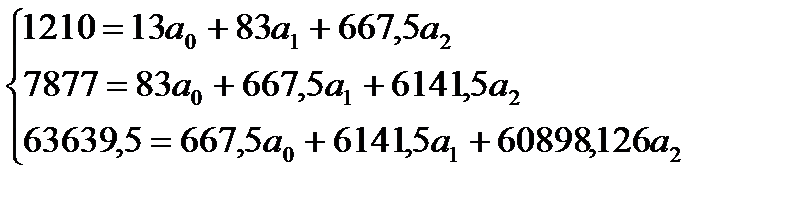
Разделим члены каждого уравнения на коэффициент при а_о

Теперь из второго уравнения вычтем первое, а из третьего - второе:

Освободимся от коэффициента при , для чего все члены уравнения разделим на коэффициент при :

Из первого уравнения вычтем второе и получим 0,727=-1,206 , отсюда а₂=-0,603. Подставим значения а₂ в уравнение 1,103= +13,668∙(-0,603); отсюда = 9,345. В уравнение 93,077 = + 6,385 + 51,346a₂ подставим значения найденных параметров и а₂:

93,077 = а₀ + 6,385∙9,345 + 51,346∙(- 0,603);

93,077 = + 59,668 - 30,962;

= 93,007 - 59,668 + 30,962;

= 64,371.

Следовательно, уравнение параболы второго порядка будет иметь следующий вид: = 64,371 + 9,345 - 0,603 .

Отрицательное значение а₂ показывает, что с увеличением возраста коров до определенного предела (6-го отела) удой возрастает на 9,345 % с каждым новым отелом, а затем после определенного предела (с 6-го отела до 12-го отела) начинает падать в среднем на 0,603 % .

Когда связь между нелинейная (в нашем случае - параболическая), для измерения тесноты связи используют корреляционное отношение, которое рассчитывается по формуле:

Полученный результат свидетельствует о наличии тесной связи между возрастом коров и их продуктивностью, так как 95,03 % вариации в продуктивности связано с возрастом данной группы коров.

Решим эту же задачу с помощью программы Statgraphics, используя в расчетах функцию Polynomial Regression (рис. 36).

Рис. 36. Результаты расчетов

Уравнение парной криволинейной зависимости примет вид: .

Случайные ошибки параметров , , равны , , 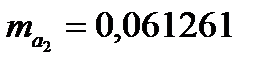. Эти значения указывают на величину, сформировавшуюся под воздействием случайных факторов. На их основе рассчитываются значения t-критерия Стьюдента: , , . На основе Приложения 2 определим критические значения t-критерия Стьюдента для уровня значимости , т.е. с вероятностью 0,95 составит 2,2281, , т.е. с вероятностью 0,99 – 3,1693. Статистически значимыми здесь являются , , .

Так как фактические значения больше теоретических (критических), то делаем вывод о существенности данных параметров ( , и ), которые формируются под воздействием не случайных причин. Об это же свидетельствует показатель вероятности случайных значений параметров регрессии, так , и То есть вероятность случайно получить такие значения t-критерия Стьюдента составляет 0,0000 %, что не превышает допустимый уровень значимости 5 %.

Чуть ниже на рис. 45 представлен расчет F-критерий Фишера, и он составляет 71,06. Согласно дисперсионному анализу вероятность получить случайно такое значение F-критерий Фишера составляет 0,0000, что не превышает допустимый уровень значимости 5%.

Отсюда же берем нескорректированный коэффициент детерминации , который оценивает долю вариации результата в зависимости от факторов в общей вариации. Этот показатель показывает на достаточно высокую связь результата и от факторного признака. Скорректированный коэффициент детерминации 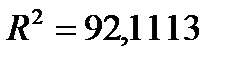оценивает тесноту связи с учетом степеней свободы общей и остаточной дисперсий. Он дает такую оценку тесноты связи, которая не зависит от числа факторов в модели и поэтому может сравниваться по разным моделям с разным числом факторов.

Задача 20. Имеются выборочные данные по 12 однородным предприятиям (табл. 32). Определите в программе Statgraphics уравнение регрессии, наиболее полно отражающее исходные данные. Оцените значимость параметров уравнения регрессии с помощью t-критерия Стьюдента и F-критерия Фишера.

Таблица 32 – Исходные данные

Построить однофакторную регрессионную модель.

Решение: воспользовавшись программой Statgraphics, получим следующие данные (табл. 33).

Таблица 33 – Уравнения регрессии, коэффициент детерминации и достоверность

№ п/п	Уравнение регрессии			P		P	F	P
		90,68	4,86	0,007	9,86	0,0000	97,26	0,0000
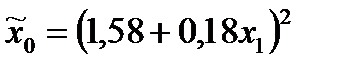
		86,59	14,01	0,0000	8,04	0,0000	64,58	0,0000
		79,63	7,83	0,0000	6,25	0,0001	39,09	0,0001
		59,81	7,92	0,0000	-3,86	0,0032	14,88	0,0032
		92,27	-1,38	0,1965	10,93	0,0000	119,4	0,0000
		93,50	-2,11	0,0608	11,99	0,0000	143,80	0,0000
		92,39	5,64	0,0002	11,02	0,0000	121,49	0,0000
		88,32	1,86	0,0932	8,70	0,0000	75,62	0,0000
		90,09	-4,93	0,0006	9,53	0,0000	90,90	0,0000
		91,44	3,01	0,0130	10,34	0,0000	106,89	0,0000
		94,13	16,46	0,0000	12,66	0,0000	160,39	0,0000
		94,14	10,30	0,0000	12,67	0,0000	160,63	0,0000
		82,45	-1,43	0,1844	6,86	0,0000	47,00	0,0000
		71,56	14,22	0,0000	-5,02	0,0005	25,17	0,0005
		88,78	30,73	0,0000	-8,90	0,0000	79,15	0,0000
		96,68	6,80	0,0000	17,08	0,0000	291,58	0,0000
		55,25	7,34	0,0000	-3,51	0,0056	12,35	0,0056
		79,81	9,12	0,0000	6,29	0,0001	39,54	0,0001
		72,60	18,18	0,0000	5,15	0,0004	26,50	0,0004
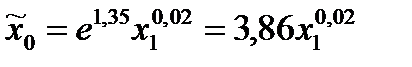
		63,14	11,73	0,0000	4,14	0,0020	17,3	0,0020
		41,68	7,49	0,0000	-2,67	0,0234	7,15	0,0234
		87,73	3,60	0,0048	8,46	0,0000	71,52	0,0000

Как видим из таблицы 5, 6, 8 и 13 уравнения отпадают, так как не соответствуют по уровню t-критерия Стьюдента. Наиболее полно отражает действительность 17 модель, так как коэффициент детерминации равен 96,68 %. Однако более точный выбор дал бы коэффициент апроксимации.