Методические советы по выполнению контрольной работы 3 страница

Мы получили следующую функцию Среднее квадратическое отклонение равно 0,02, - 0,006, - 0,023. Коэффициент детерминации составил 0,59, число степеней свободы – 4, F – статистика – 5,86, остаточная сумма квадратов – 0,002, регрессионная сумма квадратов – 0,003.

Пример решения задачи 14. По данным табл. 21 в MS Excel постройте графики и спрогнозируйте посевные площади всех сельскохозяйственных культур Чувашской Республики построив 1) линейную, 2) экспоненциальную, 3) логарифмическую, 4) полиноминальную, 5) степенную линии тренда, указав на ней функцию и коэффициент апроксимации. Определите линию тренда, наиболее полно отражающую исследуемую совокупность.

Решение:вMS Excel (Windows 7)построим диаграммы по следующей схеме:

1) выделим посевную площадь,

2) в главном меню выбираем Вставка /График. Следует обратить внимание, что во время выполнения следующих операций вы должны постоянно кликать на график,

3) находим Конструктор /Макеты диаграмм и нажимаем на нужный макет (в нашем примере первый по счету),

4) в главном меню выбираем Макет /Названия осей /Название основной горизонтальной оси /Название под осью.Заполняем названия осей («Посевная площадь, га» и «Годы»),

5) находим Конструктор /Выбрать данные и выходит диалоговое окно «Выбор источника данных». Кликаем мышкой на «Ряд 1», затем на «Изменить» с левой стороны,

Рис. 10. Диалоговое окно «Выбор источника данных»

Рис. 11. Диалоговое окно «Изменение ряда»

Заполняем Имя ряда и нажимаем дважды на ОК.

6) находим Конструктор /Выбрать данные и выходит диалоговое окно «Выбор источника данных». Кликаем мышкой на «Изменить» уже с правой стороны. Выходит новое диалоговое окно «Подписи оси» и заполняем его. Затем вновь нажимаем дважды на ОК,

Рис. 12. Диалоговое окно «Подписи оси»

7) выбираем Макет /Линия тренда /Линейное приближение. На графике появляется линия тренда. Дважды кликаем на нее и выходит диалоговое окно «Формат линии тренда».

Рис. 13. Диалоговое окно «Формат линии тренда»

Отмечаем прогноз на три года и ставим две галочки внизу. Кликаем на «Закрыть».

Более наглядно полученный график представлен на рис. 23.

Рис. 14. Линейная линия тренда

Как видно из рис. 14 линейная функция имеет вид

По аналогичной схеме построим остальные графики. Как только вы поняли, что можете строить их без подсказки, можете облегчить себе работу следующим образом. Скопировать предыдущий график, кликнуть дважды на линии тренда и менять ее параметры.

Рис. 15. Экспоненциальная линия тренда

Рис. 16. Логарифмическая линия тренда

Рис. 17. Полиноминальная линия тренда

Рис. 18. Степенная линия тренда

Внимательно сравнив графики по максимальному значению определяем, что наиболее полно исследуемую совокупность отражает экспоненциальная линия тренда.

Задачи 15 и 16 составлены по теме «Индексы. Анализ индексным методом».

Задача 15.На основе данных о продаже товаров (табл. 22) определите: 1) индивидуальные индексы объемов продаж в натуральном выражении, цен и товарооборота; 2) агрегатные индексы физического объема; 3) агрегатные индексы цен по формулам Пааше и Ласпейреса; 4) общий индекс товарооборота; 5) абсолютные приросты товарооборота за счет изменения объемов продаж, цен за счет совместного действия обоих факторов. Показать взаимосвязь между общими индексами и между абсолютными приростами товарооборота.

Таблица 22 – Исходные данные

Товары	Единица измерения	Количество	Цена, руб.
Базисный период	Отчетный период	Базисный период	Отчетный период
Картофель	кг
Молоко	л

Решение:1. По картофелю:

или 75 %.

или 115,38 %.

или 86,54 %.

По молоку:

или 90 %.

или 106,67 %.

или 96 %.

2. или 87,33 %.

То есть количество проданных товаров по двум видам в среднем снизилось на 12,67 %.

3. а) по формуле Пааше:

или 108 %.

То есть средний прирост цен на все товары составил 8 %.

б) по формуле Ласпейреса:

или 108,22 %.

То есть, если бы население приобрело товаров в отчетном периоде столько же, сколько и в базисном, то цены в среднем увеличились бы на 8,22 %.

4. или 94,32 %.

То есть товарооборот по двум товарам уменьшился на 5,68 %.

5. тыс. руб.

То есть за счет снижения среднего количества реализованных товаров выручка от продажи снизилась на 9250 тыс. руб.

по методике Пааше

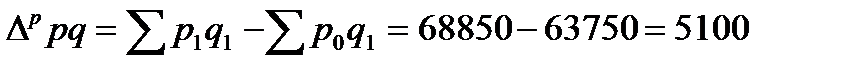тыс. руб.

Таким образом, за счет изменения среднего роста цен денежная выручка продавцов увеличилась на 5100 тыс. руб.;

по методике Ласпейреса

тыс. руб.

То есть, если население в отчетном периоде купило бы столько же товаров, что и в базисном, то в результате среднего роста цен население бы выиграло 6000 тыс. руб.;

тыс. руб.

То есть товарооборот по всем товарам сократился на 4150 тыс. руб.

Взаимосвязь (действует при условии, что индекс найден по методике Пааше) между индексами:

;

между абсолютными приростами товарооборота:

тыс. руб.

Задача 16. Имеются следующие данные о выпуске продукции «А» по двум заводам (табл. 23).

Таблица 23 – Исходные данные

№ завода	Базисный год	Отчетный год
Произведено продукции, тыс. шт.	Себестоимость единицы, руб.	Удельный вес продукции, %	Произведено продукции, тыс. шт.	Себестоимость единицы, руб.	Удельный вес продукции, %

Вычислить:

1) Индекс себестоимости переменного состава;

2) Индекс себестоимости постоянного состава;

3) Индекс структурных сдвигов

Решение: 1. Вычислим индекс себестоимости переменного состава:

или 85,45 %.

Таким образом, средняя себестоимость снизилась на 14,55 %.

2. Индекс себестоимости постоянного состава:

или 87,04 %.

Себестоимость продукции по двум заводам в среднем снизилась на 12,96 %.

3. Индекс структурных сдвигов равен:

или 98,2 %, т.е. себестоимость изделия в отчетном периоде снизилась дополнительно на 1,8 % за счет изменения структуры.

Исчисленные выше индексы можно вычислить по удельным весам продукции заводов, выраженных в коэффициентах:

а) индекс себестоимости переменного состава:

б) индекс себестоимости постоянного состава:

в) индекс структурных сдвигов:

Задачи 17…20 составлены по теме «Статистические методы изучения взаимосвязей».

Пример решения задачи 17. Охарактеризуйте зависимость урожайности зерновых от качества почвы (табл. 24), рассчитав параметры нижеследующих функций: а) линейной, б) степенной, в) экспоненты, г) показательной, д) равносторонней гиперболы, е) обратной и т.д. Определите показатели тесноты связи для каждой модели, оценив каждую из них по показателю детерминации, F-критерию Фишера, ошибку апроксимации и выбрать наилучшую из них. Для расчетов используйте программы Statgraphics,статистические функции ЛИНЕЙН, ЛГРФПРИБЛ в MS Excel, инструмент анализа данных Регрессия и т.д.

Решение: для определения формы связи между урожайностью зерновых культур и качеством почвы построим график (рис. 19). На оси абсцисс нанесем значение независимой переменной (качество почвы), на оси ординат - зависимой (урожайность).

Рис. 19. Зависимость урожайности от качества почвы

а) рассмотрим линейную функцию, выраженную уравнением прямой линии:

(34)

где - урожайность зерновых, ц/га;

- качество почвы, бал.;

- параметры уравнения связи, которые следует определить на основе решения системы нормальных уравнений с двумя неизвестными:

(35)

Для удобства расчетов заполним таблицу 24.

Таблица 24 - Данные для уравнения связи и коэффициента корреляции

№ хозяйства	Урожайность зерновых, ц/га	Качество почвы, балл	Расчетные данные	Ожидаемое значение урожайности в зависимости от качества почвы
	17,3		299,29			17,7944	-0,2737	1,582081
	17,9		320,41		751,8	18,0862	-0,2191	1,224022
	21,2		449,44			18,5239	2,5355	11,95991
	20,5		420,25			18,9616	1,2901	6,293171
	21,2		449,44		1017,6	18,9616	1,4447	6,814623
	18,6		345,96		1134,6	20,8583	-1,7007	9,143548
	19,5		380,25		1267,5	21,4419	-1,3461	6,903077
	19,8		392,04		1306,8	21,5878	-1,5915	8,037879
						22,755	2,0631	8,59625
	21,2		449,44			22,9009	-1,2823	6,048585
	19,5		380,25		1540,5	23,4845	-3,5277	18,09077
						24,214	4,4269	15,81036
	22,5		506,25		1912,5	24,3599	-1,6185	7,193333
						24,5058	-0,6639	2,76625
	24,5		600,25		2131,5	24,6517	-0,7093	2,895102
	22,5		506,25		2137,5	25,8189	-3,2547	14,46533
	24,3		590,49			26,5484	-2,0001	8,230864
	30,5		930,25			26,5484	3,6545	11,98197
	28,5		812,25			26,5484	1,1091	3,891579
	29,6		876,16			26,5484	1,6637	5,620608
Итого	455,1		10644,67		34902,3	455,1	2,1316E-14	157,5493

Данные таблицы 259 занесем в систему уравнения.

Разделив оба уравнения на коэффициент при , т.е. первое на 20, второе - на 1543, получим:

Вычтем из большего уравнения меньшее, в данном случае из второго первое:

.

Решим задачу методом определителей: определитель системы равен:

Уравнение регрессии составит:

Используя статистическую функцию ЛИНЕЙН в MS Excel (Windows 7) получим следующее решение (рис. 20).

Рис. 20. Регрессионная статистика функции ЛИНЕЙН