
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Методические советы по выполнению контрольной работы 4 страница
Чуть ниже на рис. 34 представлен расчет F-критерий Фишера, и он составляет 29,23. Согласно дисперсионному анализу вероятность получить случайно такое значение F-критерий Фишера составляет 0,0000, что не превышает допустимый уровень значимости 5%.
Отсюда же берем нескорректированный коэффициент детерминации  , который оценивает долю вариации результата в зависимости от факторов в общей вариации. Этот показатель показывает на достаточно высокую связь результата и от факторного признака. Скорректированный коэффициент детерминации
, который оценивает долю вариации результата в зависимости от факторов в общей вариации. Этот показатель показывает на достаточно высокую связь результата и от факторного признака. Скорректированный коэффициент детерминации  оценивает тесноту связи с учетом степеней свободы общей и остаточной дисперсий. Он дает такую оценку тесноты связи, которая не зависит от числа факторов в модели и поэтому может сравниваться по разным моделям с разным числом факторов.
оценивает тесноту связи с учетом степеней свободы общей и остаточной дисперсий. Он дает такую оценку тесноты связи, которая не зависит от числа факторов в модели и поэтому может сравниваться по разным моделям с разным числом факторов.
Помощью инструмента анализа данных Регрессия получим следующие данные (рис. 25).
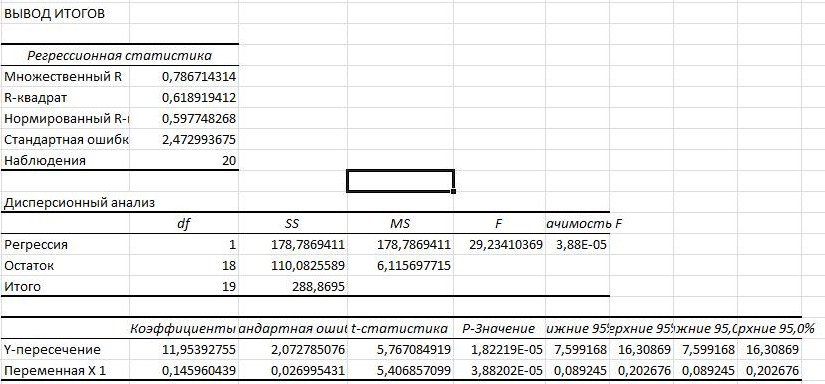
Рис. 25. Регрессионная статистика
Как видим из рис. 25 уравнение регрессии полностью совпадает.
б) рассмотрим степенную функцию:
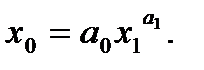 (38)
(38)
Линеаризуем модель логарифмированием:
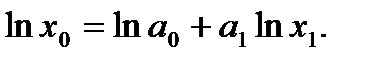
Пусть  ,
,  ,
, 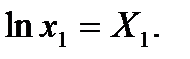
Тогда получим линейное уравнение:  .
.
Для удобства расчетов заполним таблицу 25.
Таблица 25 - Данные для уравнения связи и индекса корреляции
| № хозяйства | 
| 
| 
| 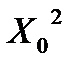
| 
| 
| 
| 
| 
|
| 2,850707 | 3,688879 | 10,51591 | 8,126528 | 13,60783 | 2,879097 | 17,7982 | 0,248206 | 29,75703 | |
| 2,884801 | 3,73767 | 10,78243 | 8,322075 | 13,97017 | 2,898926 | 18,15464 | 0,064843 | 23,57103 | |
| 3,054001 | 3,806662 | 11,62555 | 9,326923 | 14,49068 | 2,926966 | 18,67089 | 6,39639 | 2,418025 | |
| 3,020425 | 3,871201 | 11,69267 | 9,122966 | 14,9862 | 2,953195 | 19,16709 | 1,776646 | 5,085025 | |
| 3,054001 | 3,871201 | 11,82265 | 9,326923 | 14,9862 | 2,953195 | 19,16709 | 4,132719 | 2,418025 | |
| 2,923162 | 4,110874 | 12,01675 | 8,544874 | 16,89928 | 3,0506 | 21,12802 | 6,390899 | 17,26403 | |
| 2,970414 | 4,174387 | 12,39966 | 8,823362 | 17,42551 | 3,076413 | 21,68049 | 4,754532 | 10,59503 | |
| 2,985682 | 4,189655 | 12,50898 | 8,914297 | 17,55321 | 3,082618 | 21,81543 | 4,061964 | 8,732025 | |
| 3,178054 | 4,304065 | 13,67855 | 10,10003 | 18,52498 | 3,129115 | 22,85375 | 1,313896 | 1,550025 | |
| 3,054001 | 4,317488 | 13,18561 | 9,326923 | 18,6407 | 3,13457 | 22,97876 | 3,16399 | 2,418025 | |
| 2,970414 | 4,369448 | 12,97907 | 8,823362 | 19,09207 | 3,155687 | 23,46916 | 15,75425 | 10,59503 | |
| 3,332205 | 4,430817 | 14,76439 | 11,10359 | 19,63214 | 3,180628 | 24,06187 | 15,5089 | 27,51003 | |
| 3,113515 | 4,442651 | 13,83226 | 9,693978 | 19,73715 | 3,185438 | 24,17787 | 2,81526 | 0,065025 | |
| 3,178054 | 4,454347 | 14,15616 | 10,10003 | 19,84121 | 3,190191 | 24,29307 | 0,085892 | 1,550025 | |
| 3,198673 | 4,465908 | 14,28498 | 10,23151 | 19,94434 | 3,19489 | 24,40748 | 0,00856 | 3,045025 | |
| 3,113515 | 4,553877 | 14,17857 | 9,693978 | 20,73779 | 3,230641 | 25,29587 | 7,816884 | 0,065025 | |
| 3,190476 | 4,60517 | 14,69269 | 10,17914 | 21,20759 | 3,251487 | 25,82872 | 2,336998 | 2,387025 | |
| 3,417727 | 4,60517 | 15,73921 | 11,68086 | 21,20759 | 3,251487 | 25,82872 | 21,82082 | 59,98503 | |
| 3,349904 | 4,60517 | 15,42688 | 11,22186 | 21,20759 | 3,251487 | 25,82872 | 7,135714 | 33,00503 | |
| 3,387774 | 4,60517 | 15,60128 | 11,47702 | 21,20759 | 3,251487 | 25,82872 | 14,22252 | 46,85403 | |
| Итого | 62,22751 | 85,20981 | 265,8842 | 194,1402 | 364,8998 | 62,22812 | 452,4346 | 119,8099 | 288,8695 |
| В среднем | 3,111375 | 4,260491 | 13,29421 | 9,70701 | 18,24499 | 2,879097 | 17,7982 | 29,75703 |
Получим систему нормальных уравнений:
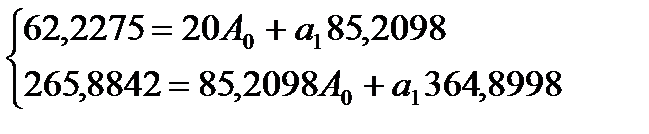
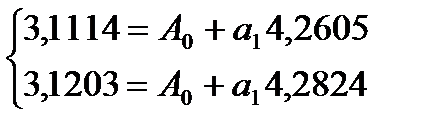
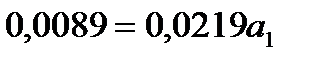
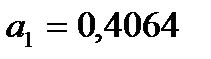
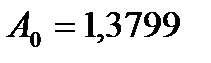
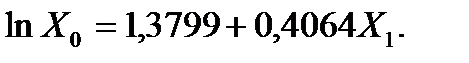
Коэффициент эластичности 0,4064 показывает, что с ростом качества почвы на 1 балл, урожайность зерновых возрастает на 0,41 ц/га.
Если решить эту систему через статистическую функцию ЛИНЕЙН в MS Excelполучим следующее уравнение
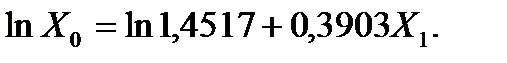
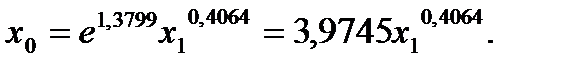
Решим эту задачу с помощью программы Statgraphics (рис. 26).
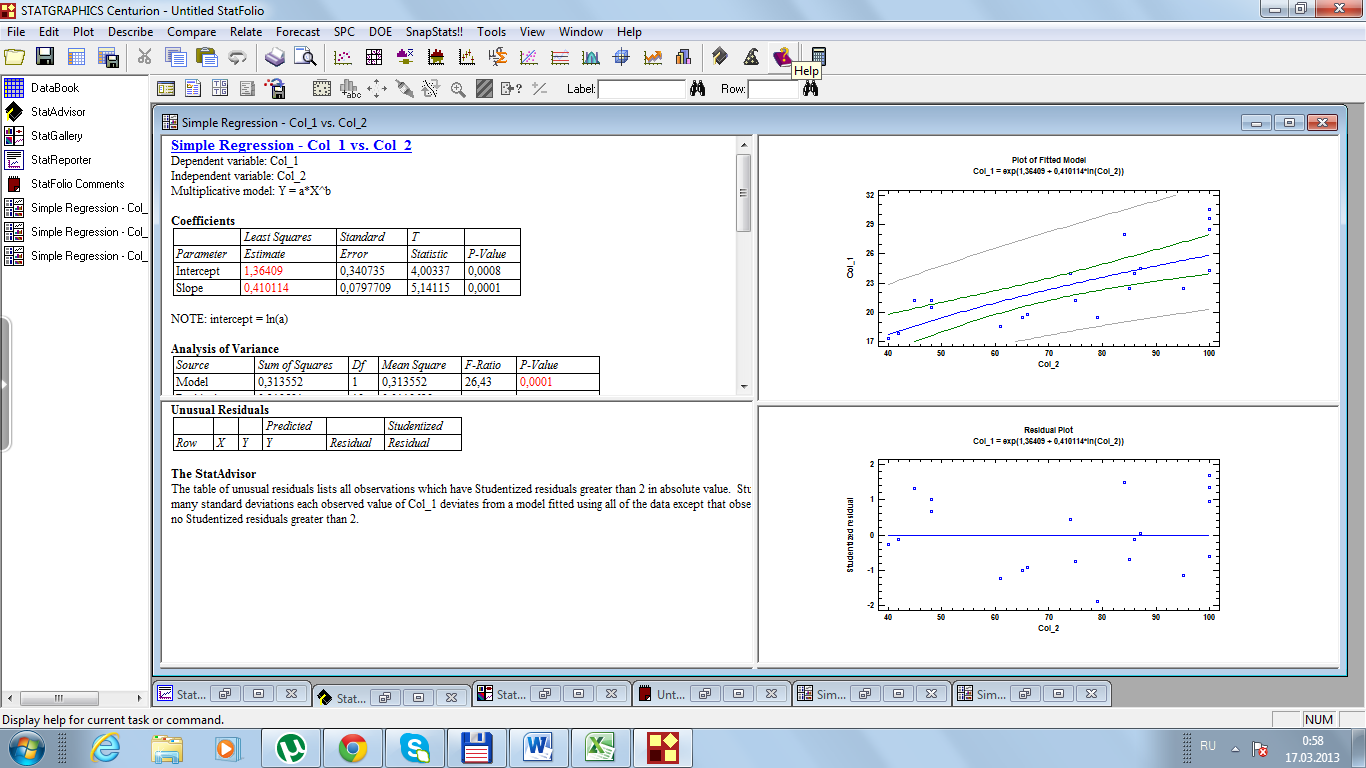
Рис. 26. Результаты расчетов
Получаем уравнение регрессии  Из рисунка 36 видно, что случайные ошибки параметров
Из рисунка 36 видно, что случайные ошибки параметров  и
и  равны
равны  и
и  . Эти значения указывают на величину, сформировавшуюся под воздействием случайных факторов. На их основе рассчитываются значения t-критерия Стьюдента:
. Эти значения указывают на величину, сформировавшуюся под воздействием случайных факторов. На их основе рассчитываются значения t-критерия Стьюдента: 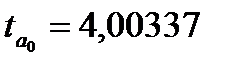 и
и  . На основе Приложения 2 определим критические значения t-критерия Стьюдента для уровня значимости
. На основе Приложения 2 определим критические значения t-критерия Стьюдента для уровня значимости  , т.е. с вероятностью 0,95 составит 2,1098,
, т.е. с вероятностью 0,95 составит 2,1098,  , т.е. с вероятностью 0,99 – 2,8982. Так как фактические значения больше теоретических (критических), то делаем вывод о существенности данных параметров (
, т.е. с вероятностью 0,99 – 2,8982. Так как фактические значения больше теоретических (критических), то делаем вывод о существенности данных параметров (  и
и  ), которые формируются под воздействием не случайных причин. Об это же свидетельствует показатель вероятности случайных значений параметров регрессии, так
), которые формируются под воздействием не случайных причин. Об это же свидетельствует показатель вероятности случайных значений параметров регрессии, так  То есть вероятность случайно получить такое значение t-критерия Стьюдента составляет 0,0000, что не превышает допустимый уровень значимости 5 %.
То есть вероятность случайно получить такое значение t-критерия Стьюдента составляет 0,0000, что не превышает допустимый уровень значимости 5 %.
Тесноту связи определим, рассчитав индекс корреляции:
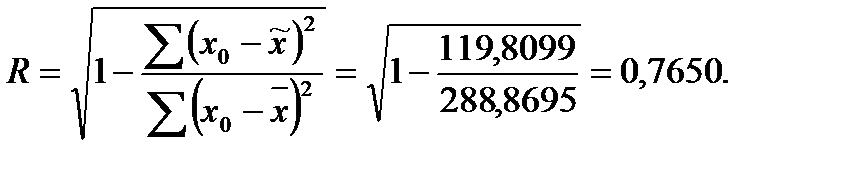
Коэффициент детерминации составил 0,5852, таким образом, на 58,52% вариации  объясняется вариацией
объясняется вариацией  , на долю прочих факторов приходится 23,5 %.
, на долю прочих факторов приходится 23,5 %.
Рассчитаем F-критерий Фишера по формуле:
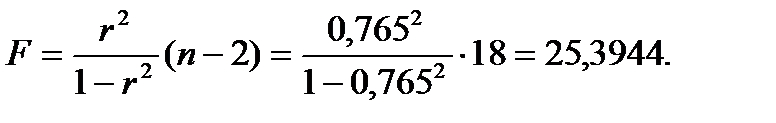
Табличное значение F-критерий Фишера составило 4,41. Так как фактическое значение F превышает табличное, уравнение регрессии  статистически значимо.
статистически значимо.
Чуть ниже (рис. 36) представлен расчет F-критерий Фишера, и он составляет 26,43. Согласно дисперсионному анализу вероятность получить случайно такое значение F-критерий Фишера составляет 0,0001, что не превышает допустимый уровень значимости 5%.
Определим среднюю ошибку апроксимации по формуле:
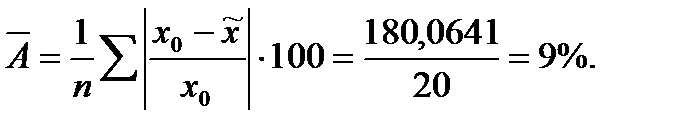
Этот показатель не выше 8 - 10 %, т.е. среднее отклонение расчетных  и фактических
и фактических  данных не столь велико.
данных не столь велико.
в) рассмотрим функцию экспоненты:
 (39)
(39)
Для оценки параметров приведем уравнение к линейному виду:
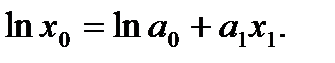
Воспользуемся методом наименьших квадратов и получим систему уравнений:

Для удобства расчетов заполним таблицу 26.
Таблица 26 - Данные для уравнения связи и индекса корреляции
| № хозяйства | 
| 
| 
| 
| 
| 
| 
| 
| 
|
| 0,0578 | 2,3121 | 114,0283 | 18,0970 | 0,6352 | 29,757 | 0,0461 | |||
| 0,0559 | 2,3464 | 121,1616 | 18,3279 | 0,1831 | 23,571 | 0,0239 | |||
| 0,0472 | 2,1226 | 137,4301 | 18,67984 | 6,3512 | 2,4180 | 0,1189 | |||
| 0,0488 | 2,3415 | 144,9804 | 19,03853 | 2,1360 | 5,0850 | 0,0713 | |||
| 0,0472 | 2,2642 | 146,5921 | 19,03853 | 4,6720 | 2,4180 | 0,1020 | |||
| 0,0538 | 3,2796 | 178,3129 | 20,67416 | 4,302147 | 17,2640 | 0,1115 | |||
| 0,0513 | 3,3333 | 193,0769 | 21,20516 | 2,90762 | 10,5950 | 0,0874 | |||
| 0,0505 | 3,3333 | 197,055 | 21,34003 | 2,3717 | 8,7320 | 0,0778 | |||
| 0,0417 | 3,0833 | 235,176 | 22,45032 | 2,4015 | 1,5500 | 0,0646 | |||
| 0,0472 | 3,5378 | 229,0501 | 22,5931 | 1,9407 | 2,4180 | 0,0657 | |||
| 0,0513 | 4,0513 | 234,6627 | 23,1734 | 13,4938 | 10,5950 | 0,1884 | |||
| 0,0357 | 279,9052 | 23,9198 | 16,6484 | 27,5100 | 0,1457 | ||||
| 0,0444 | 3,7778 | 264,6488 | 24,0719 | 2,4708 | 0,0650 | 0,0699 | |||
| 0,0417 | 3,5833 | 273,3126 | 24,2250 | 0,0506 | 1,5500 | 0,0094 | |||
| 0,0408 | 3,5510 | 278,2846 | 24,3791 | 0,0146 | 3,0450 | 0,0049 | |||
| 0,0444 | 4,2222 | 295,784 | 25,6475 | 9,9065 | 0,0650 | 0,1399 | |||
| 0,0413 | 4,1152 | 319,0476 | 26,4735 | 4,7242 | 2,3870 | 0,0894 | |||
| 0,0328 | 3,2787 | 341,7727 | 26,4735 | 16,2126 | 59,9850 | 0,1320 | |||
| 0,0351 | 3,5088 | 334,9904 | 26,4735 | 4,1067 | 33,0050 | 0,0711 | |||
| 0,0338 | 3,3784 | 338,7774 | 26,4735 | 9,7749 | 46,8540 | 0,1056 | |||
| Итого | 0,9024 | 64,4208 | 4658,049 | 452,7551 | 105,3042 | 288,8695 | 1,7255 |
Получим систему нормальных уравнений:

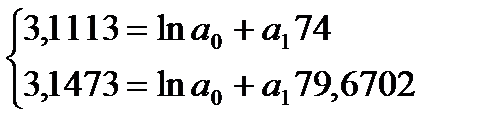
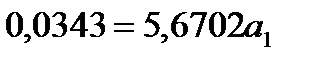
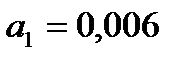
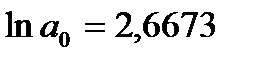
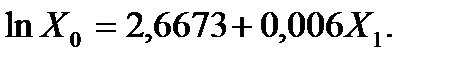
Сделаем потенцирование
 .
.
Тесноту связи определим, рассчитав индекс корреляции:
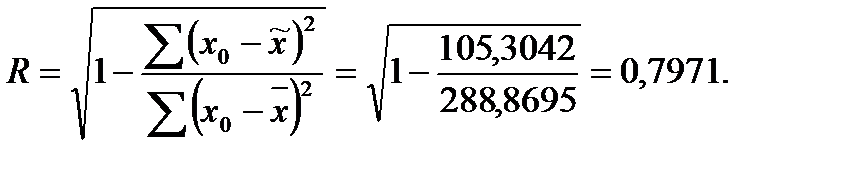
Коэффициент детерминации составил 0,6365, таким образом, на 63,65 % вариации  объясняется вариацией
объясняется вариацией  , на долю прочих факторов приходится 36,47 %.
, на долю прочих факторов приходится 36,47 %.
Рассчитаем F-критерий Фишера по формуле:
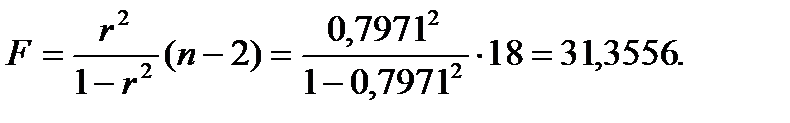
Табличное значение F-критерий Фишера составило 4,41. Так как фактическое значение F превышает табличное, уравнение регрессии  статистически значимо.
статистически значимо.
Определим среднюю ошибку апроксимации по формуле:

Этот показатель не выше 8 - 10 %, т.е. среднее отклонение расчетных  и фактических
и фактических  данных не столь велико.
данных не столь велико.
Решим эту задачу с помощью программы Statgraphics (рис. 27).
Таким образом, мы получили те же значения и уравнение регрессии  . Из рисунка 37 видно, что случайные ошибки параметров
. Из рисунка 37 видно, что случайные ошибки параметров  и
и  равны
равны  и
и  . На их основе рассчитываются значения t-критерия Стьюдента:
. На их основе рассчитываются значения t-критерия Стьюдента:  и
и  . На основе Приложения 2 определим критические значения t-критерия Стьюдента для уровня значимости
. На основе Приложения 2 определим критические значения t-критерия Стьюдента для уровня значимости  , т.е. с вероятностью 0,95 составит 2,1098,
, т.е. с вероятностью 0,95 составит 2,1098,  , т.е. с вероятностью 0,99 – 2,8982. Так как фактические значения больше теоретических (критических), то делаем вывод о существенности данных параметров (
, т.е. с вероятностью 0,99 – 2,8982. Так как фактические значения больше теоретических (критических), то делаем вывод о существенности данных параметров (  и
и  ), которые формируются под воздействием не случайных причин. Об это же свидетельствует показатель вероятности случайных значений параметров регрессии, так
), которые формируются под воздействием не случайных причин. Об это же свидетельствует показатель вероятности случайных значений параметров регрессии, так  То есть вероятность случайно получить такое значение t-критерия Стьюдента составляет 0,0000, что не превышает допустимый уровень значимости 5 %.
То есть вероятность случайно получить такое значение t-критерия Стьюдента составляет 0,0000, что не превышает допустимый уровень значимости 5 %.
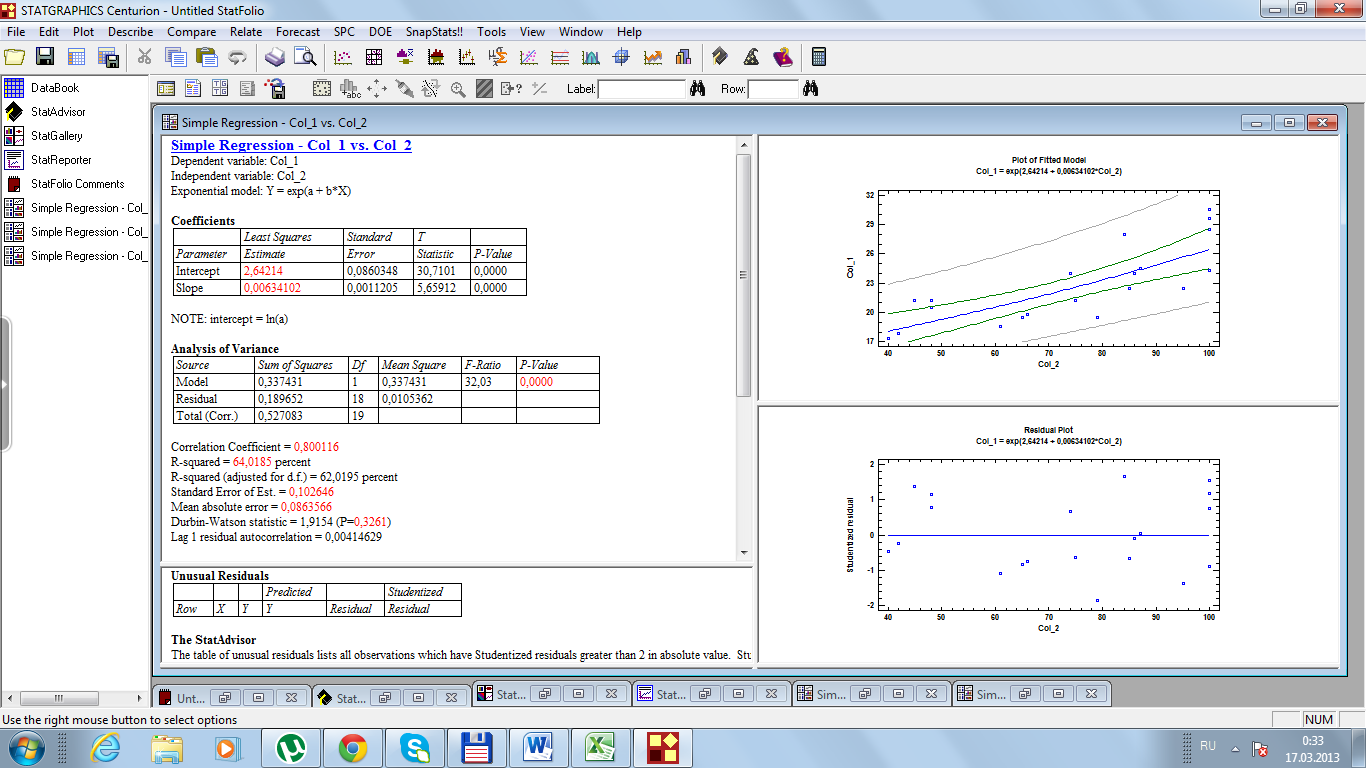
Рис. 27. Результаты расчетов
Чуть ниже на рис. 28 представлен расчет F-критерий Фишера, и он составляет 32,03. Согласно дисперсионному анализу вероятность получить случайно такое значение F-критерий Фишера составляет 0,0000, что не превышает допустимый уровень значимости 5%.
г) рассмотрим функцию показательной кривой:
 (40)
(40)
Для оценки параметров приведем уравнение к линейному виду:
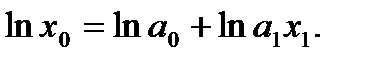
Воспользуемся методом наименьших квадратов и получим систему уравнений:
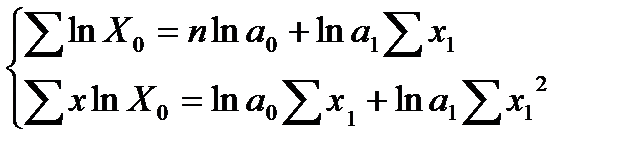
Получим систему нормальных уравнений:
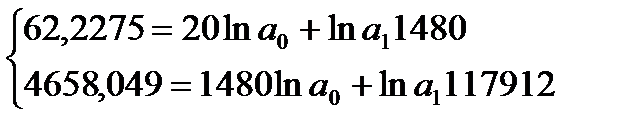
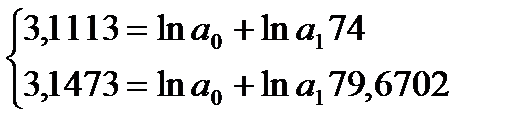
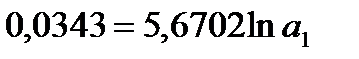
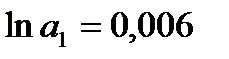
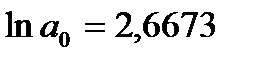
Получаем уравнение регрессии:
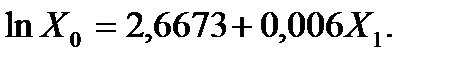
Сделаем потенцирование и получим
 ;
; 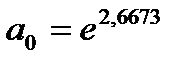 ;
;  ,
,  , получаем
, получаем
 .
.
Тесноту связи определим, рассчитав индекс корреляции:
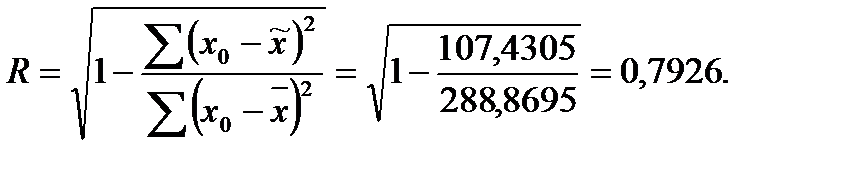
Коэффициент детерминации составил 0,6282, таким образом, на 62,82% вариации  объясняется вариацией
объясняется вариацией  , на долю прочих факторов приходится 37,18 %.
, на долю прочих факторов приходится 37,18 %.
Рассчитаем F-критерий Фишера по формуле:
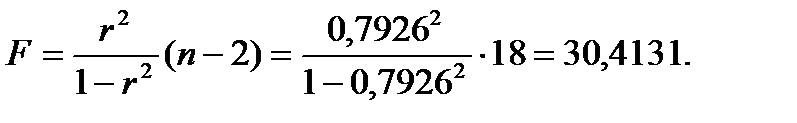
Табличное значение F-критерий Фишера составило 4,41. Так как фактическое значение F превышает табличное, уравнение регрессии 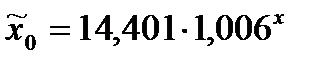 статистически значимо.
статистически значимо.
Определим среднюю ошибку апроксимации по формуле:
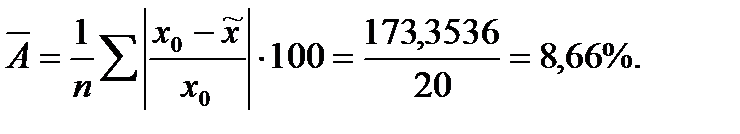
Этот показатель не выше 8 - 10 %, т.е. среднее отклонение расчетных  и фактических
и фактических  данных не столь велико.
данных не столь велико.
Эту задачу решим с помощью статистической функции ЛГРФПРИБЛ (рис. 28).
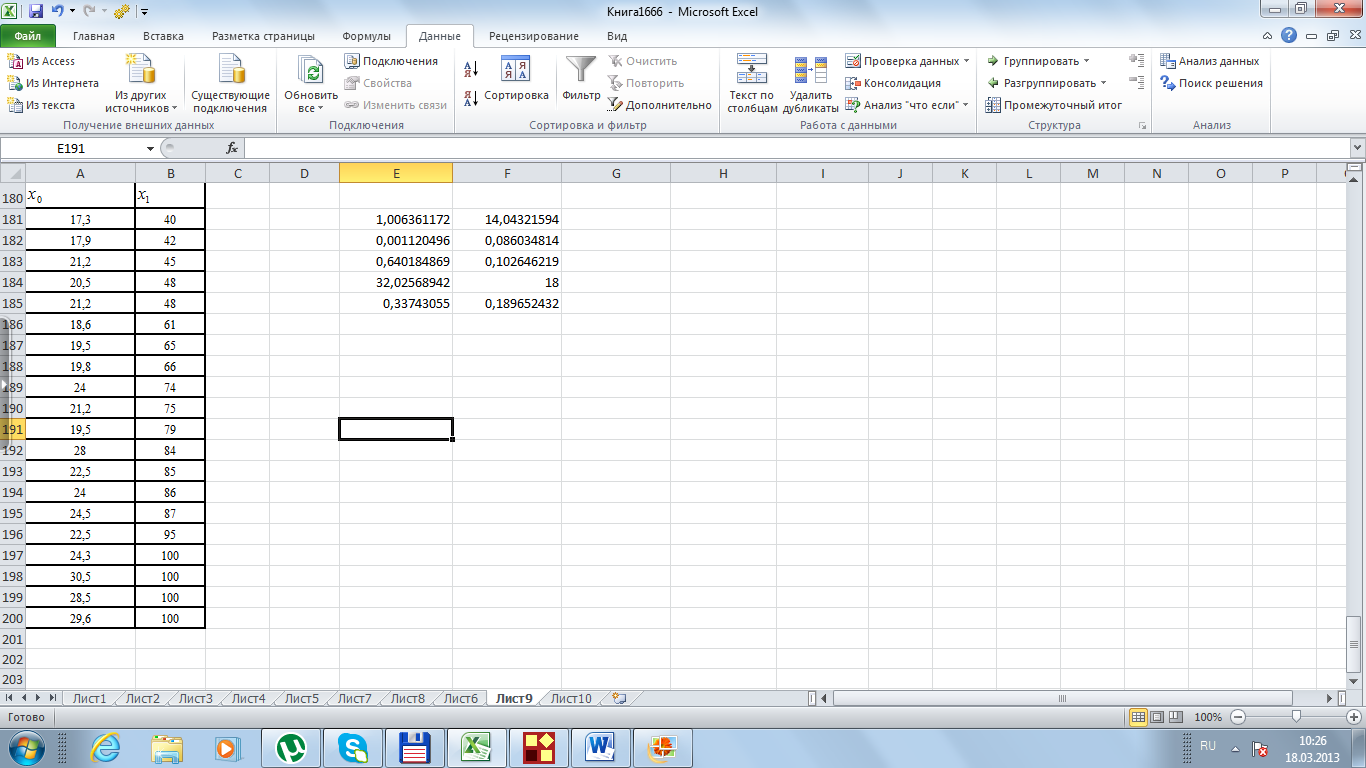
Рис. 28. Решение статистической функции ЛГРФПРИБЛ
Таким образом, мы получаем уравнение регрессии  .
.
д) рассмотрим функцию равносторонней гиперболы:
 . (41)
. (41)
Для оценки параметров приведем уравнение к линейному виду при  . Затем получим
. Затем получим 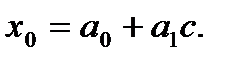
Воспользуемся методом наименьших квадратов и получим систему уравнений:
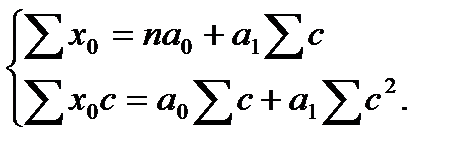
Таблица 27 - Данные для уравнения связи и коэффициента корреляции
| № хозяйства | 
| 
| 
| 
| 
| 
| 
|
| 17,3 | 0,025 | 0,4325 | 0,000625 | 17,39276 | 0,00860349 | -0,53616 | |
| 17,9 | 0,0238095 | 0,42619 | 0,000567 | 18,0186 | 0,01406483 | -0,66254 | |
| 21,2 | 0,0222222 | 0,47111 | 0,000494 | 18,85305 | 5,508179518 | 11,07052 | |
| 20,5 | 0,0208333 | 0,42708 | 0,000434 | 19,5832 | 0,84052988 | 4,472215 | |
| 21,2 | 0,0208333 | 0,44167 | 0,000434 | 19,5832 | 2,614055713 | 7,626435 | |
| 18,6 | 0,0163934 | 0,30492 | 0,000269 | 21,91727 | 11,00429439 | -17,8348 | |
| 19,5 | 0,0153846 | 0,3 | 0,000237 | 22,44762 | 8,688454595 | -15,116 | |
| 19,8 | 0,0151515 | 0,3 | 0,00023 | 22,57016 | 7,673789783 | -13,9907 | |
| 0,0135135 | 0,32432 | 0,000183 | 23,43127 | 0,32345658 | 2,369718 | ||
| 21,2 | 0,0133333 | 0,28267 | 0,000178 | 23,52599 | 5,410226379 | -10,9716 | |
| 19,5 | 0,0126582 | 0,24684 | 0,00016 | 23,8809 | 19,19225154 | -22,4661 | |
| 0,0119048 | 0,33333 | 0,000142 | 24,277 | 13,86074673 | 13,29644 | ||
| 22,5 | 0,0117647 | 0,26471 | 0,000138 | 24,35063 | 3,424816156 | -8,225 | |
| 0,0116279 | 0,27907 | 0,000135 | 24,42254 | 0,178541624 | -1,76059 | ||
| 24,5 | 0,0114943 | 0,28161 | 0,000132 | 24,4928 | 5,17738E-05 | 0,029369 | |
| 22,5 | 0,0105263 | 0,23684 | 0,000111 | 25,00165 | 6,258276422 | -11,1185 | |
| 24,3 | 0,01 | 0,243 | 0,0001 | 25,27834 | 0,957153069 | -4,0261 | |
| 30,5 | 0,01 | 0,305 | 0,0001 | 25,27834 | 27,26571227 | 17,12019 | |
| 28,5 | 0,01 | 0,285 | 0,0001 | 25,27834 | 10,37908027 | 11,30406 | |
| 29,6 | 0,01 | 0,296 | 0,0001 | 25,27834 | 18,67672787 | 14,6002 | |
| Итого | 455,1 | 0,296451 | 6,48186 | 0,004868 | 454,862 | 142,2790129 | -24,819 |
Получим систему нормальных уравнений:
Дата добавления: 2014-12-23; просмотров: 303; Мы поможем в написании вашей работы!; Нарушение авторских прав |