Ряды динамики и их виды.

Все общественные явления, изучаемые статистикой, изменяются во времени. Эти изменения исследуются с помощью динамических (временных) рядов. Ряд расположенных во времени статистических данных, изменение которых отражает закономерность развития изучаемого явления, называется рядом динамики или временным рядом.

Ряд динамики представляет собой числовые значения определенного статистического показателя в последовательные моменты или периоды времени.

Числовые значения того или иного статистического показателя, составляющие ряд динамики, называют уровнями ряда и обычно обозначают через y. Моменты или периоды времени, к которым относятся уровни, обозначают через t.

Таким образом временной ряд состоит из двух элементов:

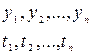, где y_{i –} уровень ряда, t_i - дата, или временной интервал.

В зависимости от вида показателей ряды динамики подразделяют на ряды абсолютных, относительных и средних величин (показателей). На основе рядов абсолютных величин образуются ряды динамики относительных и средних величин. Ряды относительных величин могут характеризовать темпы роста или снижения определенного показателя, уровень рождаемости или смертности, примером ряда средних величин служат данные о среднегодовой численности занятых в экономике, о средней заработной плате и др.

Временные ряды могут быть интервальными и моментными. Моментным называется ряд, уровни которого характеризуют значение показателя (явления) по состоянию на определенные моменты времени (дату).

Интервальнымназывается ряд, уровни которого характеризуют значение показателя, достигнутое за определенный период (интервал).

2. Показатели рядов динамики.

Большинство статистических характеристик ряда динамики основано на абсолютном или относительном сравнении его уровней. Сравниваемый уровень принято называть текущим, а уровень, с которым производится сравнение, - базисным.

Показатели роста и приростапредназначены для характеристики изменения уровней ряда (y_t ). Показатели роста представляют собой отношение двух уровней, а прироста - их разность. Если эти показатели имеют вид относительных величин, их называют коэффициентами. Если они выражены в процентах - темпами.

Они могут быть цепными и базисными. У цепных ведется сравнение текущего уровня с предыдущим, а у базисных - с начальным, принятым за базу.

В качестве базисного выбирается либо начальный уровень ряда, либо уровень, с которого начинается какой-то новый этап развития явления.

Абсолютное изменение уровней ряда измеряется показателем абсолютного прироста.

Цепные показатели прироста исчисляются так: D_2ц = y₂ - y₁ D_3ц = y₃ - y₂ D _4ц = y₄ - y₃ . . . D _iц = y_i - y_i-1

Базисные показатели прироста: D_2б = y₂ - y₁ D_3б = y₃ - y₁ D_4б = y₄ - y₁ . . . D_iб = y_i - y₁

Абсолютный прирост характеризует увеличение или уменьшение уровня ряда за определенный промежуток времени. Абсолютные приросты с переменной базой (цепные) называют скоростью роста или первыми разностями.

Цепные и базисные абсолютные приросты связаны между собой: сумма последовательных цепных абсолютных приростов равна базисному, то есть общему приросту за весь промежуток времени.

Для характеристики интенсивности, то есть относительного изменения уровня динамического ряда за какой-либо период времени исчисляют коэффициенты или темпы роста (снижения). Цепные коэффициенты ростаисчисляются следующим образом:

К_2/1ц = К_3/2ц = К_4/3ц = 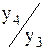. . . К_i/i-1ц =

Цепные темпы роста будут иметь следующий вид: Т_2/1ц=(K_2/1ц)100%, T_3/2ц= (K_3/2ц)100%, ….

Базисные коэффициенты роста будут такими:

К_2/1б = К_3/1б = К_4/1б = . . . К_i/1б =

Базисные темпы роста: T_2/1б=(K_2/1б)100%, T_3/2б=(K_3/2б)100% …

Они показывают во сколько раз сравниваемый уровень больше уровня, с которым производится сравнение (если коэффициент больше 1) или какую часть уровня, с которым производится сравнение, составляет сравниваемый уровень (если он меньше единицы).

Между цепными и базисными коэффициентами роста существует взаимосвязь (если базисные коэффициенты исчислены по отношению к начальному уровню ряда динамики): произведение последовательных цепных коэффициентов роста равно базисному коэффициенту роста за весь период, а частное от деления последующего базисного коэффициента роста на предыдущий уровень равно соответствующему цепному коэффициенту роста.

Относительную оценку скорости изменения уровня ряда в единицу времени дают показатели коэффициентов (темпов) прироста. Темп приростапоказывает на сколько процентов сравниваемый уровень больше или меньше уровня, принятого за базу сравнения. Он представляет собой отношение абсолютного прироста к предыдущему или начальному (базисному) уровню.

Т _пр.ц.=(åDy_ц/y_i-1)100% T _пр.б.=( Dy_б/y₁)100%

Темп прироста можно получить и из темпа роста, выраженного в процентах, если из него вычесть 100%. Коэффициент прироста получается вычитанием 1 из коэффициента роста.

При анализе динамики развития следует так же знать какие абсолютные значения скрываются за темпами роста и прироста. Сравнение абсолютного прироста и темпа прироста за одни и те же периоды времени показывает, что при снижении темпов прироста абсолютный прирост не всегда уменьшается, в отдельных случаях он может возрастать. Поэтому, чтобы правильно оценить значение полученного темпа прироста, его рассматривают в сопоставлении с показателем абсолютного прироста. Результат выражают показателем, который называют абсолютным значением (содержанием) одного процента приростаи рассчитывают как отношение абсолютного прироста к темпу прироста за тот же период времени, %:

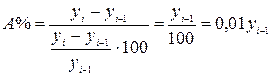
В тех случаях, когда сравнение производится с отдалением периода времени, принятого за базу сравнения, рассчитывают, так называемые, пункты роста, которые представляют собой разность базисных темпов (при)роста, %, двух смежных периодов.

3. Средние показатели ряда динамики.

С делением рядов на моментные и интервальные непосредственно связан способ расчета их среднего уровня. Средний уровень интервального ряда с равными интервалами исчисляется по формуле простой арифметической:

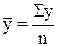
Средний уровень моментного ряда исчисляется по формуле средней хронологической:

где y₁ и y_n - начальный и конечный уровни ряда,

y₂ , y₃ . - промежуточные уровни,

n - число уровней ряда, принимаемых в расчет.

Чем больше промежуточных уровней участвует в расчете, тем точнее характеризуется средний уровень ряда. Когда же их нет, тогда средний уровень ряда исчисляют только по концам ряда.

Средний абсолютный прирост рассчитывается по формулам: ,

где - абсолютные цепные приросты; - количество абсолютных цепных приростов.

Или , где у_n – конечный уровень ряда; у₁ – первоначальный уровень ряда; n – общее число уровней ряда.

Средний абсолютный прирост показывает, на сколько в среднем увеличивается (уменьшается) изучаемое явление.

Средний темп (коэффициент) роста или прироста позволяет оценить среднюю скорость изменения уровней временного ряда. Средний коэффициент роста исчисляется с помощью средней геометрической простой или взвешенной. Взвешенная используется тогда, когда значения некоторых коэффициентов роста повторяются.

Средняя геометрическая простая: , где К₁, К₂, К₃ ... К_n - цепные коэффициенты роста за n периодов.

Или .

Средняя геометрическая взвешенная имеет такой вид:

.

Средняя геометрическая взвешенная может иметь такой вид: , где К_i - цепной коэффициент роста в i-том периоде, w_i - вес i-того периода, исчисляемый как . Причем обязательно Sw_i =1.

4. Проблемы сопоставимости и приемы преобразования временных рядов

Преобразование временных рядоввключает в себя приемы, позволяющие сделать ряды более удобными для анализа. В частности, оно включает в себя такие приемы, как приведение рядов к одному основанию и смыкание рядов.

Приведение рядов к одному основаниюпозволяет лучше увидеть, какой ряд растет быстрее, а какой медленнее. К этому приему приходится прибегать тогда, когда сравниваемые ряды имеют разные начальные периоды, исчислены в разной валюте или имеют другие различия, затрудняющие их непосредственное сравнение.

Для приведения рядов к одному основанию выбирается один, общий для всех рядов начальный период, который берется за 100%.

Смыкание временных рядов.К этому приему приходится прибегать тогда, когда надо создать один длинный, сквозной ряд из нескольких коротких рядов, отличающихся либо методологией расчета показателей, либо границами территории, либо ценами, что не позволяет их соединить вместе без всяких пересчетов. Смыкание рядов может быть осуществлено только в том случае, если ряды имеют хотя бы один общий период.