Методы анализа основной тенденции развития в рядах динамики.

На развитие явлений по времени оказывают влияние факторы различные по характеру и силе воздействия. Некоторые из них носят случайный характер, другие оказывают практически постоянное воздействие и формируют в рядах динамики определенную тенденцию развития.

Важной задачей статистики является выявление в рядах динамики тренда, освобожденного от действия различных случайных факторов. С этой целью ряды динамики подвергаются обработке методами укрупнения интервалов, скользящей средней и аналитического выравнивания и др.

Метод укрупнения интервалов основан на укрупнении периодов времени, к которым относятся уровни ряда динамики, т.е. представляет из себя замену данных, имеющих отношение к мелким временным периодам, данными по более крупным периодам. Особенно эффективен, когда первоначальные уровни ряда относятся к коротким промежуткам времени. Например, ряды показателей, относящиеся к ежедневным событиям, заменяются рядами, относящимся к недельным, помесячным и т.д. Это позволит более отчетливо показать «ось развития явления». Средняя, исчисленная по укрупненным интервалам, позволяет выявлять направление и характер (ускорение или замедление роста) основной тенденции развития.

Метод скользящей среднейсхож с предыдущим, но в данном случаефактические уровнизаменяются средними уровнями, рассчитанными для последовательно подвижных (скользящих) укрупненных интервалов, охватывающих m уровней ряда.

Например, если принять m=3,то вначале рассчитывается средняя из первых трех уровней ряда, затем – из такого же числа уровней, но начиная со второго по счету, далее – начиная с третьего и т.д. Таким образом, средняя как бы «скользит» по ряду динамики, передвигаясь на один срок. Рассчитанные из mчленов скользящие средние относятся к середине (центру) каждого интервала.

Этот метод устраняет лишь случайные колебания. Если же ряд имеет сезонную волну, то она сохранится и после сглаживания методом скользящей средней.

Аналитическое выравнивание. В целях устранения случайных колебаний и выявления тренда применяется выравнивание уровней ряда по аналитическим формулам (или аналитическое выравнивание). Его суть состоит в замене эмпирических (фактических) уровней теоретическими , которые рассчитаны по определенному уравнению, принятому за математическую модель тренда, где теоретические уровни рассматриваются как функция времени: . При этом каждый фактический уровень рассматривается как сумма двух составляющих: , где - систематическая составляющая и выраженная определенным уравнением, а - случайная величина, вызывающая колебания вокруг тренда.

Задача аналитического выравнивания сводится к следующему:

1. Определение на основе фактических данных вида гипотетической функции , способной наиболее адекватно отразить тенденцию развития исследуемого показателя.

2. Нахождение по эмпирическим данным параметров указанной функции (уравнения)

3. Расчет по найденному уравнению теоретических (выровненных) уровней.

Выбор той или иной функции осуществляется, как правило, на основе графического изображения эмпирических данных.

В качестве моделей служат уравнения регрессии, параметры которых рассчитывают по способу наименьших квадратов

Ниже приводятся наиболее часто используемые для выравнивания динамических рядов уравнения регрессии с указанием для отражения каких именно тенденций развития они наиболее всего подходят.

Вид уравнения	Отражаемая уравнением тенденция развития
Уравнение прямой	Равномерный рост при b1>0 или равномерное падение при b1 < 0
Показательная функция	Ускоряющийся рост при b1>1 или замедляющееся падение при b1<1
Гипербола	Замедляющееся падение при b1 > 0 или замедляющийся рост при b1 < 0
Парабола	Рост, переходящий в падение, или падение, переходящее в рост в точке t =

Для нахождения параметров приведенных выше уравнений существуют специальные алгоритмы и компьютерные программы. В частности для нахождения параметров уравнения прямой может быть использован такой алгоритм:

Если периоды или моменты времени пронумеровать так, чтобы получилось St =0, то вышеприведенные алгоритмы существенно упростятся и превратятся в

Выровненные уровни на графике расположатся на одной прямой, проходящей на самом близком расстоянии от фактических уровней данного динамического ряда. Сумма квадратов отклонений является отражением влияния случайных факторов. С ее помощью рассчитаем среднюю (стандартную) ошибку уравнения:

Здесь n - число наблюдений, а m - число параметров в уравнении ( их у нас два – b₁ и b₀).

Основная тенденция (тренд) показывает, как воздействуют систематические факторы на уровни ряда динамики, а колеблемость уровней около тренда ( 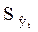) служит мерой воздействия остаточных факторов.

Для оценки качества используемой модели динамического ряда применяется также критерий F Фишера. Он представляет из себя отношение двух дисперсий, а именно отношение дисперсии, вызванной регрессией, т.е. изучаемым фактором, к дисперсии, вызванной случайными причинами, т.е. остаточной дисперсией:

В развернутом виде формула этого критерия может быть представлена так:

где n - число наблюдений, т.е. число уровней ряда,

m - число параметров в уравнении, y - фактический уровень ряда,

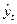- выровненный уровень ряда, 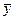- средний уровень ряда.

Более удачная, чем другие, модель не всегда может оказаться достаточно удовлетворительной. Ее можно признать таковой только в том случае, когда критерий F у нее перешагнет известную критическую границу. Эта граница устанавливается с помощью таблиц F-распределения.