Средний арифметический и средний гармонический индексы, тождественные агрегатному

Агрегатная форма индекса является основной определяющей формой. Но не всегда можно воспользоваться именно этой формой индекса. Например, если нет данных о количестве проданных товаров, то индекс физического объема по агрегатной формуле исчислить нельзя. Но его можно построить в форме средней величины из соответствующих индивидуальных индексов.

Рассмотрим преобразование агрегатного индекса в средний арифметический на примере индекса физического объема продукции:

Это индекс Ласпейреса, т.к. сооизмерители взяты на уровне базисного периода. Знаменатель этого индекса обычно известен. Индексируемый показатель в числителе индекса ( ) можно заменить через соответствующий индивидуальный индекс ( ).

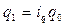
Подставив в числитель агрегатного индекса вместо выражение , получим:

Таким образом, мы получили средний арифметический индекс физического объема продукции.

Агрегатный индекс качественных показателей можно преобразовать в гармоническую форму индекса. Для преобразования воспользуемся агрегатным индексом цен (индекс Пааше):

В этом индексе числитель – величина известная, в знаменателе р₀ можно заменить через индивидуальный индекс цен: .

Подставляем в знаменатель индекса вместо p₀ равное ему выражение . Получаем следующую формулу индекса цен:

Этот индекс является средним гармоническим взвешенным индексом цен,

Аналогично, путем простых подстановок, можно получить средний гармонический индекс себестоимости 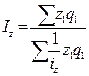и средний гармонический индекс трудоемкости

В преобразованных индексах теперь уже числитель остается неизменным и слагаемое числителя появляется в знаменателе. Таким образом, средний гармонический индекс будет тождествен агрегатному в том случае, если весами обратных значений индивидуальных индексов будут взяты слагаемые числителя агрегатного индекса.

Средний гармонический индекс цен находит широкое применение при расчете индексов розничных цен. Что же касается, например, индекса себестоимости, то он исчисляется, как правило, по агрегатной формуле, т.к. на предприятиях имеется количественный учет произведенной продукции.