Ряды индексов с постоянной и переменной базой сравнения (цепные и базисные), с постоянными и переменными весами

Изменение социально-экономических явлений очень часто изучают не за два периода, а за более длительный отрезок времени (три, четыре, пять и более периодов). В этих случаях возникает проблема выбора базы сравнения. В зависимости от базы сравнения различают цепные и базисные индексы.

Цепные индексы- это индексы, имеющие переменную, т.е. меняющуюся базу сравнения.

Базисные индексы- это такие индексы, в которых база сравнения не меняется, остается постоянной.

Цепные и базисные индексы подразделяются на индивидуальные и общие (сводные) индексы.

Методика построения индивидуальных индексов (и цепных, и базисных) очень проста. Возьмем несколько последовательных периодов (годы): 2000, 2001, 2002, 2003, 2004.

Для построения индивидуальных индексов количества продукции введем соответствующие обозначения: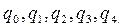

Построим за пять последовательных периодов цепные индивидуальные индексы количества продукции:

.

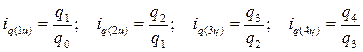За эти же периоды построим базисные индивидуальные индексы количества продукции:

.

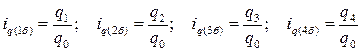Между цепными и базисными индексами существует взаимосвязь, позволяющая переход от одних индексов к другим, заключается она в следующем: произведение всех цепных индексов равно соответствующему базисному индексу (индексу последнего периода):

.

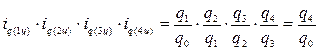Из этой взаимосвязи следует: отношение каждого последующего базисного индекса к предшествующему базисному индексу позволяет получить соответствующий (промежуточный) цепной индекс.

Важно отметить, что рассмотренная взаимосвязь цепных индексов всегда проявляется в индивидуальных индексах, а в сводных индексах – только в случае постоянства весов (соизмерителей).

Чтобы рассмотреть методику построения сводных цепных индексов, воспользуемся агрегатной формой индекса физического объёма продукции.

Допустим, нам известны цены взятых выше пяти периодов: .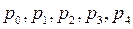

Построим ряд сводных цепных индексов физического объема продукции с постоянными весами - соизмерителями (р₀):

.

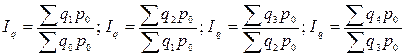При перемножении этих индексов можно получить общий базисный индекс.

Построим ряд сводных цепных индексов физического объема продукции с переменными весами:

.

В зависимости от целей исследования и характера исходной информации, рассмотренные нами сводные цепные индексы можно представить как индексы с постоянными и переменными весами.

Два и более индексов с одинаковыми по содержанию и во времени весами (соизмерителями) представляют собой ряд индексов с постоянными весами-соизмерителями:

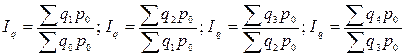
Два и более индексов с одинаковыми по содержанию, но различными во времени весами (соизмерителями) образуют ряд индексов с переменными весами-соизмерителями:

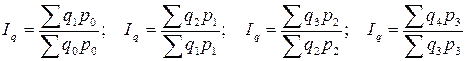
В статистической практике более предпочтительно использование индексов с постоянными весами (соизмерителями). Так, например, индекс физического объема валового внутреннего продукта (ВВП) вычисляется по формуле Ласпейреса:

.

В качестве постоянных базисных цен (р₀) используются текущие цены года, принятого за базу сравнения. Цены обновляются каждые пять лет.

Индекс физического объема ВВП - один из важнейших макроэкономических показателей, используемый в современной статистике для характеристики социально-экономического развития страны в целом, а также отдельных отраслей экономики и регионов.