Виды и формы связей, различаемые в статистике

Различают два типа взаимосвязей между различными явлениями и их признаками: жестко детерминированную и стохастически детерминированную.

Функциональная жестко детерминированная связь– это вид причинной зависимости, при которой определенному значению факторного признака соответствует одно или несколько точно заданных значений результативного признака. Этот вид связи встречается чаще в естественных наука.

Стохастическая связь – это вид причинной зависимости, проявляющейся не каждом отдельном случае, а в общем, среднем, при большом числе наблюдений.

Среди взаимосвязанных признаков одни могут рассматриваться как определенные факторы, влияющие на изменение других, а вторые как следствие, результат влияния первых. Соответственно первые, то есть признаки, влияющие на изменение других, называют факторными, а вторые – результативными. Стохастические взаимосвязи могут быть изучены различными способами. Наиболее известный из них метод изучения корреляционных связей.

Корреляционная связь- частный случай стохастической связи, состоящей в том, что c изменением факторного признака (х) закономерным образом изменяется среднее значение результативного признака (y), в то время как в каждом отдельном случае y может принимать множество различных значений. Отсюда задача измерения силы корреляционной связи состоит в нахождении меры совместной вариации двух признаков.

Корреляционная связь между признаками может возникать различными путями. Важнейший путь – взаимосвязь вариации результативного признака с вариацией факторного признака. Обычно в этом случае говорят о взаимосвязи признаков.

Корреляционная связь может возникнуть между двумя следствиями общей причины. В таком случае мы можем оценить, так называемую, ложную корреляцию.

Корреляция возникает и в случае, когда каждый из признаков и причина, и следствие.

По направлению выделяют связь прямую и обратную(положительную и отрицательную), По аналитическому выражению линейную и нелинейную.

2. Измерение тесноты связи в случае корреляционной зависимости

Большинство методов измерения тесноты связи заключается в сопоставлении отклонений значений признаков от их средних. Это основано на предположении, что при полной независимости признаков отклонения значений факторного признака от средней носят случайный характер и должны случайно сочетаться с различными отклонениями . При наличии значительного перевеса совпадений или несовпадений таких отклонения делается предположение о наличии связи между х и y.

Самый известный измеритель тесноты связи между признаками - линейный коэффициент парной корреляции Пирсона, характеризующий тесноту и направление связи между двумя признаками в случае наличия между ними линейной зависимости.

Коэффициент корреляции Пирсона находится через коэффициент ковариации (среднее значение совместных отклонений признаков от их средних значений):

Это – мера совместной вариации признаков. Или можно сказать, что это – мера соответствия вариации результативного признака вариации факторного. Недостатком коэффициента ковариации является то, что он не нормирован. Для преодоления этого недостатка полученное выражение разделим на среднее квадратическое отклонение по х и по y.

Полученное значение – линейный коэффициент парной корреляции Пирсона, показатель интенсивности (силы) линейной связи. Это - безразмерная величина, которая изменяется в интервале от –1 до +1, .

Качественная оценка степени интенсивности связи между признаками производится по шкале Чеддока

Критерии оценки тесноты связи линейного коэффициента парной корреляции К.Пирсона

Значения коэффициента корреляции	до
Характеристика тесноты связи	слабая	умеренная	заметная	Высокая	достаточно высокая

Путем ряда преобразований можно получить следующие аналитические выражения для коэффициента корреляции:

, где , или

Производя расчет по итоговым значениям исходных переменных, линейный коэффициент корреляции можно вычислить по формуле:

.

3. Оценка достоверности коэффициента корреляции

Коэффициент линейной корреляции, исчисленный по выборочным данным является случайной величиной. Полученный из выборки коэффициент корреляции r является оценкой коэффициента корреляции r в генеральной совокупности. С уменьшением числа наблюдений надежность коэффициента корреляции падает. Оценка существенности (значимости) линейного коэффициента корреляции основана на сопоставлении значения r с его средней квадратической ошибкой : . При оценке значимости коэффициента корреляции обычно рассматриваются следующие ситуации.

Оценка достоверности (значимости) коэффициента корреляции

Характеристики коэффициента корреляции	Средняя квадратическая ошибка	Вывод о значимости коэффициента корреляции делается, если:
Большое число наблюдений, распределение приближенно нормальное, r < 0,9
Малое число наблюдений (n < 30), распределение далеко от нормального, r < 0,9		, где находится по таблице распределения Стьюдента с параметрами
Малое число наблюдений (n < 30), распределение далеко от нормального, r > 0,9		, где z – преобразование Фишера

Задавшись определенной вероятностью, можно построить доверительные границы r:

.

где - генеральное значение коэффициента корреляции; - заданный уровень вероятности.

4. Ранговая корреляция

В анализе социально-экономических явлений широко используются ранговые коэффициенты корреляции (коэффициенты корреляции рангов), когда коррелируют не непосредственные значения X и Y, а их ранги, т.е. номера их мест, занимаемых в каждом ряду значений по возрастанию или убыванию. К таким коэффициентам относятся коэффициенты рангов Спирмена и Кендэлла.

Если nвариантов рядарасположены в соответствии с возрастанием или убыванием признака х, то говорят, что объекты ранжированы по этому признаку. Ранг для х_i указывает место, которое занимает i-е значение признака среди других n значений признака х (i=1,2,..n).

Для данных примера 6.15

Коэффициент ранговой корреляции Спирмена,расчет которого основан на различиях между рангами. Обозначим D = ранг A – ранг B.

, где n – число пар ранжированных наблюдений.

Коэффициент Спирмена изменяется в интервале от [-1; 1] и интерпретируется так же как и коэффициент Пирсона.

Значимость коэффициента Спирмена проверяется на основе t критерия Стьюдента по формуле:

.

Значение коэффициента считается существенным, если t_расч. > t_крит. (a; k = n-2).

Коэффицент корреляции рангов (при условии, что ранги не повторяются) может быть рассчитан и по формуле, предложенной английским статистиком М. Кендаллом:

, где S- фактическая сумма рангов; - максимальная сумма рангов.

Этот коэффициент изменяется в интервале от [-1;1] –и интерпретируется так же как и коэффициент Пирсона, но он дает более строгую оценку связи, чем коэффициент Спирмена 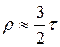. Это соотношение выполняется при большом числе наблюдений, 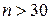, и слабых, либо умеренно тесных связях.

При расчете коэффициента Кендалла соблюдается следующая последовательность действий:

Значения ранжируются в порядке возрастания или убывания.

Значения располагаются в порядке соответствующем значениям .

Для каждого ранга определяется число следующих за ним значений рангов, превышающих его величину. Результат записывается в столбец «+», суммируется и обозначается Р.

Для каждого ранга определяется число следующих за ним меньших значений рангов. Результат записывается в столбец «-», суммируется и обозначается Q.

Определяется общая сумма S=P+Q.

Значимость коэффициента корреляции рангов Кендалла проверяется по формуле:

,

где t_α- коэффициент, определяемый по таблице нормального распределения для выбранного уровня значимости α при больших n.

5. Корреляция альтернативных признаков

Альтернативные признаки – это признаки, принимающие только два возможных значения. Исследования их корреляции основано на показателях, построенных на четырехклеточных таблицах, в которые сводятся значения признаков.

Для измерения тесноты взаимосвязи таких признаков производится расчет коэффициентов контингенции и ассоциации:

;

Коэффициенты принимают значения на интервале [-1; 1]. Интерпретация аналогична коэффициенту корреляции. Коэффициент контингенции всегда бывает меньше коэффициента ассоциации и дает более корректную оценку тесноты связи.