
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Методические указания по изучению дисциплины
«Сценарий изучения» дисциплины «Основы статистики» включает разъяснения по следующим основным моментам.
Лекции и практические занятия. Во 2 семестре для очной формы обучения организуются лекции и практические занятия. Их цель - обратить внимание на общую схему построения соответствующего раздела курса, подчеркнуть важнейшие факты. На этих занятиях могут быть разобраны более подробно отдельные вопросы курса, которые недостаточно освещены в рекомендованных пособиях.
Чтение учебника. Изучая материал по учебнику [основной: Ниворожкина Л.И. Статистика: Учебник для бакалавров / Л.И. Ниворожкина, [и др.]; под общ. ред. д.э.н., проф. Л.И. Ниворожкиной – М.: Издательско-торговая корпорация «Дашков и К», 2010. – 416 с], следует переходить к следующему вопросу только после понимания предыдущего. Особое внимание надо обратить на основные понятия курса. Нужно подробно разобрать примеры, поясняющие такие определения. При изучении учебника полезно вести конспект, в который выписываются определения, формулы, уравнения и т.д. На полях конспекта отмечаются вопросы, выделенные для консультации с преподавателем. Многим студентам помогает составление листа, содержащего важнейшие и наиболее употребляемые формулы курса.
Решение задач. При решении задач нужно обосновывать каждый этап решения. Полезно до начала вычислений составить краткий план решения. Решение задач и примеров надо записывать подробно, располагать вычисления в строгом порядке, отделяя вспомогательные вычисления от основных. Решение каждой задачи надо доводить до окончательного ответа, по возможности в общем виде с выводом формулы. Затем в полученную формулу подставляются числовые значения входящих в нее величин. В завершении необходимо дать комментарии и сделать выводы по полученным результатам.
Самопроверка. После изучения определенной темы рекомендуется воспроизвести по памяти определения, выводы формул, формулировки и доказательства теорем, проверяя себя по учебнику. Иногда недостаточность усвоения вопроса выясняется только при изучении дальнейшего материала. В этом случае надо вернуться назад и повторить нужный раздел. Важным критерием усвоения теории является умение решать задачи на пройденный материал. Но будет ошибкой считать благополучное решение задач признаком усвоения теории. Часто правильное решение задач получается в результате применения механически заученных формул.
Контрольные работы: Контрольные работы дают студенту возможность судить об усвоении им соответствующего модуля курса, выявить имеющиеся пробелы. К выполнению контрольного задания можно приступить после того как решено достаточное количество задач по соответствующему модулю. Все выполняемые задания должны быть выполнены студентом самостоятельно. Если это условие нарушено, то студент не приобретает необходимых компетенций и оказывается не подготовленным к экзамену.
Завершающим этапом является сдача зачёта. При подготовке к зачёту студент руководствуется списком вопросов, а также использует рекомендованную литературу.
Зачёт сдается в письменной форме. Зачётное задание содержит 10 тестовых вопросов и 1 задачу. На выполнение письменной работы отводится 2 академических часа. По окончании времени, отведенного для письменного ответа, работа сдается преподавателю, который проверяет ее, задает уточняющие вопросы и выставляет оценку. Сдача зачёта проходит в один из дней зачётной недели, во время, согласованное преподавателем со студентами и учебной частью. Пересдача неудовлетворительных оценок происходит по направлениям деканата, в соответствии с установленным графиком пересдач.
На зачёте выясняется усвоение всех теоретических и прикладных вопросов программы и умение применять знания к решению прикладных задач. Определения, правила должны формулироваться точно, с пониманием существа дела, задачи в простейших случаях нужно решать без ошибок и уверенно. Решение задач во время итогового контроля является ОБЯЗАТЕЛЬНЫМ условием получения положительной оценки. Только в этом случае знания студента ОЦЕНИВАЮТСЯ ПОЛОЖИТЕЛЬНО.
Методические указания по выполнению практических работ
Задачи для самостоятельного решения и решения на практических занятиях приводятся в следующих источниках основной литературы:
[5] Ниворожкина Л.И. Статистика: Учебник для бакалавров / Л.И. Ниворожкина, [и др.]; под общ. ред. д.э.н., проф. Л.И. Ниворожкиной – М.: Издательско-торговая корпорация «Дашков и К», 2010. – 416 с.
[7] Ниворожкина Л. И., Рудяга А. А., Федосова О. Н. Теория статистики. Практикум./ Рост. гос. эконом. универ. «РИНХ».– Ростов н/Д, 2005.– 185 с.
[14] Яковлева Н.А. Теория статистики: практикум / Н.А. Яковлева; Рост. гос. эконом. ун-т (РИНХ). – Ростов н/Д., 2010. – 76 с.
Ниже приведены решения типовых задач по каждой теме дисциплины.
Модуль 1 «Теоретические и организационные основы статистики»
Тема «Предмет, метод, задачи и организация статистики»
Какими признаками по классификации, приведенной ниже, являются: розничный товарооборот торговых объединений, этажность жилых помещений и состояние в браке.
Решение: Основания классификации представлены в таблице.
| По характеру их выражения | По способу измерения | По отношению к характеризуемому объекту | По характеру вариации | По отношению ко времени |
| Описательные (качественые) | Первичные или учитываемые | Прямые (непосредственные) | Альтернативные | Моментные |
| Количественные | Вторичные расчетные | Косвенные | Дискретные | Интервальные |
| Непрерывные |
Итак, признак «розничный товарооборот торговых объединений» - количественный, вторичный, прямой, непрерывный, интервальный.
Признак «этажность жилых помещений» - количественный, первичный, прямой, дискретный.
Признак «состояние в браке» - описательный, первичный, прямой, альтернативный, моментный.
Тема «Статистическое наблюдение»
Требуется провести обследование потребительских ожиданий населения (по данным Росстата). Определите цели и задачи исследования, объект и предмет исследования, критический момент наблюдения. [4]
Решение.
При проведении предлагаемого исследования необходимо, прежде всего, определить, что собственно является предметом статистического интереса. В зависимости от потребностей в информации о названном сегменте рынка, интерес исследователя может быть направлен на различные цели.
Например, целью статистического исследования потребительских ожиданий населения может быть выбрано определение особенностей изменения потребительских ожиданий различных групп населения России.
В соответствии с поставленной целью должны быть определены следующие задачи исследования:
− изучение мнения населения о динамике общей экономической ситуации;
− изучение мнения населения о динамике личного материального положения;
− изучение мнения населения о рынках товаров/услуг и сбережений;
− расчет частных и обобщающих показателей потребительских ожиданий;
− исследование потребительского поведения и потребительских предпочтений населения;
− анализ особенностей потребительских ожиданий отдельных социально-демографических групп населения.
Выделение объекта наблюдения связано с определением совокупности единиц – носителей определенных признаков.
В качестве объекта наблюдения выделяем совокупность населения России в возрасте 16 лет и старше, так как младшие категории населения не влияют в значительной степени на платёжеспособный спрос.
Единица наблюдения – отдельный взрослый индивид. Причем статистической единицей − респондентом является член конкретного домашнего хозяйства. То есть, на первом этапе выделения единиц наблюдения производят отбор домашних хозяйств, и только затем определяют лиц, которые будут опрошены.
Конкретные домашние хозяйства для участия в опросе ежеквартально определяются территориальными органами государственной статистики методом случайного отбора в соответствии с рекомендациями по объему и структуре выборочной совокупности, разработанными Росстатом в разрезе регионов.
В каждом домохозяйстве опрашивается только один человек. Отбор респондента для опроса осуществляется «методом последнего дня рождения». Это означает, что в опросе участвует тот взрослый член домохозяйства, чей прошедший день рождения был ближайшим ко дню проведения опроса.
Предметом исследования являются потребительские ожидания населения России в возрасте 16 лет и старше. Круг признаков, характеризующих предмет исследования, определяется в соответствии с задачами исследования. Например, должны быть зафиксированы (в соответствующей шкале) мнение индивида о предстоящем направлении и интенсивности изменения общей экономической ситуации и доходов обследуемого домохозяйства, цен (по видам товарных рынков), ассортимента предлагаемых товаров и услуг. Кроме того, непременно должны быть зафиксированы основные социально-демографические признаки респондента, чтобы обеспечить возможность типологизации населения и построения аналитических группировок.
По указанным признакам будет произведен расчет системы показателей для совокупности в целом и ее отдельных социально-демографических групп.
По охвату наблюдением единиц совокупности данное обследование является несплошным, организованным как выборочное.
По способу наблюдения − экспедиционное как формализованное персональное интервью по месту жительства респондентов.
По систематичности наблюдения данное обследование потребительских ожиданий населения относится к текущим, организуемым ежеквартально в 88 субъектах Российской Федерации.
Тема «Сводка и группировка данных статистического наблюдения»
В результате статистического опроса получены данные о заработной плате 30 специалистов коммерческих банков (тыс. руб.):
| 22, 45, 36, 17, 24, 39, 40, 44, 55, 72, 77, 56, 27, 41, 40, 31, 33, 18, 55, 64, 67, 70, 34, 21, 20, 47, 30, 29, 47, 51 |
Решение: Сделать какие-либо выводы из исходных данных не представляется возможным. Строить дискретный вариационный ряд также нерационально, так как он будет иметь большое число значений с частотами равными единице. Более правильно построить интервальный вариационный ряд. Для этого воспользуемся формулой Стерджесса и определим величину интервала

Учитывая, что минимальное значение признака 17, образуем первый интервал, прибавив к минимальному значению величину интервала 10, то есть нижняя граница первого интервала 17, а верхняя 27, второй интервал соответственно 27-37 и т.д. Таким образом, получим интервалы 17-27, 27-37, 37-47, 47-57, 57-67, 67-77.
Ранжируем исходные данные:
| 17, 18, 20, 21, 22, 24, 27, 29, 30, 31, 33, 34, 36, 39, 40, 40, 41, 44, 45, 47, 47, 51, 55, 55, 56, 64, 67, 70, 72, 77 |
Подсчитаем частоты. При подсчете возникает ситуация, в которой вариант (например 27) попадает на границу интервалов и может быть отнесен как к более раннему интервалу, так и к следующему за ним. В этом случае следует отнести его к интервалу, на верней границе которого он находится. Таким образом, 27 относится к первому интервалу. Результаты построения интервального вариационного ряда запишем в виде таблицы:
Распределение специалистов коммерческих банков
по величине заработной платы
| Величина заработной платы, тыс. руб. | Количество специалистов, чел. |
| 17-27 | |
| 27-37 | |
| 37-47 | |
| 47-57 | |
| 57-67 | |
| 67-77 | |
| Итого |
Модуль 2. «Методы измерения массовых социально-экономических явлений»
Тема «Абсолютные и относительные статистические показатели»
Имеются следующие данные о распределении населения по полу.
Распределение населения по полу за 1980 – 1997 годы
| Годы | Численность населения на начало года, тыс. чел. | в том числе | |
| мужское | Женское | ||
| 138 127 | 63 610 | 74 517 | |
| 147 662 | 69 112 | 78 555 | |
| 147 938 | 69 486 | 78 455 | |
| 147 137 | 69 029 | 78 108 |
По этим данным исчислите соотношение численности мужчин и женщин, а также удельные веса мужчин и женщин в населении. Укажите, к какому виду относительных показателей структурных соотношений относятся исчисленные показатели.
Решение: 1) отношение численности мужского населения к численности женского – это относительный показатель координации:

Т.е. в 1980 г. на 1000 женщин приходилось 850 мужчин, в 1990 г. – 880 и т.д.
2) удельный вес мужчин (женщин) в общей численности рассчитывается как относительный показатель структуры:

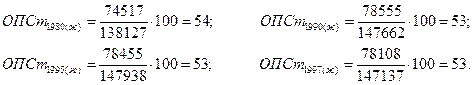
Т.е. в 1980 г. доля мужчин в общей численности населения составляла 46%, а доля женщин соответственно 54%; в 1990, 1995 и 1997 годах данные соотношения были одинаковыми и находились на уровне 47% (доля мужчин) и 58% (доля женщин).
Пусть требуется определить средний размер двух видов вклада в банке в октябре и ноябре ХХ года по данным следующей таблицы:
| Вид вклада | Октябрь | Ноябрь | ||
| Число вкладов, тыс. f | Средний размер вклада, тыс. руб. x | Сумма вкладов, млн. руб. M | Средний размер вклада, тыс. руб. x | |
| До востребования | 4,07 | |||
| Срочный | 3,87 |
Решение: В октябре известен средний размер вкладов каждого вида х и количество вкладов f. Следовательно, для расчета среднего размера вклада по двум видам применяем формулу средней арифметической взвешенной, тыс. руб.:

В ноябре известен средний размер вкладов каждого вида, а количество вкладов не известно, но зато имеются данные об общих суммах вкладов.
Путем деления сумм вкладов М каждого вида на их средний размер вклада х можно определить веса – число вкладов по их видам f, а затем определить средний размер вклада по двум видам по формуле средней арифметической.
Если в расчете использовать среднюю гармоническую, то отпадает необходимость предварительного расчета весов – размеров вкладов по каждому виду, поскольку эта операция заложена в саму формулу. Средняя гармоническая взвешенная применяется, когда статистическая информация не содержит частот f по отдельным единицам совокупности, а представлена как произведение xf. Чтобы исчислить среднюю, обозначим xf=М, откуда f=w/x. Преобразуем формулу средней арифметической так, чтобы по имеющимся данным x и М можно было исчислить среднюю.
В формулу средней арифметической взвешенной вместо xf подставим М, вместо f – отношение М/x и получим формулу средней гармонической взвешенной:

Итак, средний размер вклада в ноябре по двум их видам находим по формуле средней гармонической взвешенной, тыс. руб.:

Тема: «Измерение вариации».
Рассчитать дисперсию, коэффициент детерминации и эмпирическое корреляционное отношение по данным таблицы.
Группировка населения отдельных областей России по среднему размеру ежемесячных денежных льгот пенсионеров в 2004 году
| Место проживания | Средний размер денежных льгот

| Численность пенсионеров, тыс.чел.

| Дисперсия льгот в области (группе) 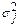
|
| Курская обл. Курганская обл. Камчатская обл. | 264,3 310,4 490,4 | 341,4 235,5 38,9 | |
| Итого | 296,2 | 615,8 | 7171,2 |
Решение: Найдем средний размер льгот по трем областям в целом:
 руб.
руб.
Вариация льгот по отдельным областям, обусловленная различием в местах проживания пенсионеров, характеризуется межгрупповой дисперсией:

Средняя из групповых дисперсий дает обобщающую характеристику случайной вариации, обусловленную отдельными факторами, кроме места проживания пенсионеров (например, характером занятости, стажем работы и т.п.):

Вариация льгот в изучаемых областях России, обусловленная влиянием всех факторов, вместе взятых, определяется общей дисперсией:

отсюда

Полученный коэффициент детерминации показывает, что дисперсия льгот зависит от места проживания пенсионеров на 32,5 %. Остальные 67,5% определяются множеством других неучтенных факторов.

Полученное значение эмпирического корреляционного отношения позволяет утверждать, что существует заметная связь между местом проживания пенсионеров и размером льгот.
Модуль 3 «Методы анализа социально-экономических процессов»
«Изучение динамики общественных явлений»
По данным примера темы «Абсолютные и относительные статистические показатели» о о распределении населения по полу рассчитать цепные и базисные темпы роста для общей численности населения, мужского и женского населения.
Решение. Расчетные данные представлены в таблице.
Показатели динамики численности населения за 1980 – 1997 годы
| Годы | Темпы роста общей численности населения | Темпы роста мужского населения | Темпы роста женского населения | |||
| цепные | базисные | цепные | базисные | цепные | базисные | |
| - | 100% | - | 100% | - | 100% | |

| 
| 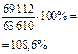
| 
| 
| 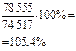
| |

| 
| 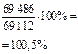
| 
| 
| 
| |

| 
| 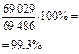
| 
| 
| 
|
Переведя темпы роста в коэффициенты, убедимся во взаимосвязи показателей с переменной и постоянной базой сравнения. Так, для всего населения получим:

«Индексы»
Допустим, имеются данные о реализации товаров какой-либо фирмы за два периода.
| Товары | 1 квартал | 2 квартал | ||
| Продано, тыс. кг. | Цена 1 кг., руб. | Продано, тыс. кг. | Цена 1 кг., руб. | |
| А Б | 42,0 30,0 | 40,0 20,0 | ||

| 
| 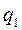
| 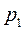
|
1. Определить общие агрегатные индексы:
а) цен по формулам Пааше и Ласпейреса;
б) физического объема товарооборота (в сопоставимых ценах);
в) товарооборота (в фактических ценах).
2. Рассчитать абсолютное изменение общей суммы товарооборота за счет изменения цен и количества реализованных товаров.
3.. Показать взаимосвязь между исчисленными индексами.
Решение:
1. а) Агрегатный индекс цен Пааше исчисляется по формуле:
 ;
;  или 127,3%
или 127,3%
Агрегатный индекс цен Ласпейреса исчисляется по формуле:
 ;
; 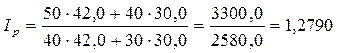 или 127,9%
или 127,9%
По формуле Пааше цены на реализованные фирмой товары во 2 квартале по сравнению с 1-ым выросли в среднем на 27,3% (127,3 - 100,0), а по формуле Ласпейреса - на 27,9% (127,9 - 100,0). Индекс Паше показывает влияние изменения цен на стоимость товаров, реализованных в отчетном периоде, а индекс Ласпейреса - на стоимость товаров реализованных в базисном периоде.
б) Агрегатный индекс физического объема товарооборота (количества
проданных товаров) в сопоставимых ценах исчисляется по формуле:
 ,
,  или 85,3%
или 85,3%
Количество проданных товаров во 2 квартале по сравнению с 1-ым снизилось на 14,7% (85,3-100,0).
в) Агрегатный индекс товарооборота (в фактических ценах) можно вычислить по формуле:
 ,
, 
 или 108,5%
или 108,5%
Товарооборот (выручка от продажи) в отчетном периоде по сравнению с базисным, т.е. во 2 квартале по сравнению с 1-ым, возрастает на 8,5% (108,5-100,0).
2. Абсолютное изменение общей суммы товарооборота исчисляется как разность между числителем и знаменателем агрегатного индекса
товарооборота:  = 2800,0 - 2580,0 = +220,0тыс. руб.
= 2800,0 - 2580,0 = +220,0тыс. руб.
Прирост товарооборота обусловлен влиянием цен и количества реализованных товаров.
Прирост товарооборота за счет изменения цен по индексу Пааше составил:
 = 2800,0 – 2200,0 = +600,0 тыс.руб.
= 2800,0 – 2200,0 = +600,0 тыс.руб.
За счет изменения количества проданных товаров произошло снижение товарооборота:
 = 2200,0 – 2580,0= - 380,0 тыс.руб.
= 2200,0 – 2580,0= - 380,0 тыс.руб.
Общее изменение товарооборота равно сумме приростов (снижения) за счет изменения цен и за счет изменения количества продаж. Итак, общий абсолютный прирост товарооборота ( 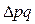 ) представлен в данном случае индексной аддитивной моделью (аддитивный-получаемый путем сложения:
) представлен в данном случае индексной аддитивной моделью (аддитивный-получаемый путем сложения: 
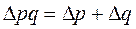 ).
).
Сделаем проверку исчисленных показателей. Результат ( 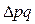 ) должен быть равен 220,0 тыс. руб.:
) должен быть равен 220,0 тыс. руб.: 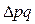 = +600,0 + (-380,0) = +220,0 тыс. руб. Следовательно, увеличение товарооборота на 220,0 тыс. руб. произошло за счет роста цен на 600,0 тыс. руб. и за счет сокращения количества реализованных товаров на 380,0 тыс. руб.
= +600,0 + (-380,0) = +220,0 тыс. руб. Следовательно, увеличение товарооборота на 220,0 тыс. руб. произошло за счет роста цен на 600,0 тыс. руб. и за счет сокращения количества реализованных товаров на 380,0 тыс. руб.
3. Между исчисленными индексами существует определенная взаимосвязь, которая может быть представлена индексной мультипликативной моделью.
Индекс представляет собой мультипликативную модель, если он может быть рассчитан в виде произведения двух, как в нашем примере, или нескольких определяющих его индексов:
 ;
;  =1,2727·0,8527=1,0852 или 108,5%.
=1,2727·0,8527=1,0852 или 108,5%.
Следует заметить, что если индекс цен рассматривается в системе с индексом физического объема и индексом товарооборота, то он должен вычисляться по формуле Пааше.
Любой недостающий индекс можно определить, пользуясь формулой взаимосвязи индексов.
Это можно подтвердить следующими расчетами. Определяем индекс цен:  ;
;  или 127,3%
или 127,3%
Определяем индекс физического объема товарооборота:

 или 85,3%.
или 85,3%.
«Изучение взаимосвязи общественных явлений»
Для изучения влияния условий труда на взаимоотношения в коллективе было проведено выборочное обследование 250 работников предприятия, ответы которых распределились следующим образом:
| Условия труда | Взаимоотношения в коллективе | |||
| Хорошие | Удовлетворительные | Неудовлетворительные | Итого | |
| Соответствуют требованиям | ||||
| Не полностью соответствуют | ||||
| Не соответствуют | ||||
| Итого |
Требуется охарактеризовать связь между исследуемыми показателями с помощью коэффициента взаимной сопряженности К.Пирсона.
Решение: Коэффициент взаимной сопряженности К.Пирсона определяется по формуле:
 , где
, где  - показатель средней квадратической сопряженности.
- показатель средней квадратической сопряженности.

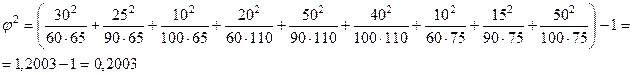
 .
.
Полученное значение коэффициента сопряженности свидетельствует, что связь между условиями труда и взаимоотношениями в коллективе умеренная.
Дата добавления: 2014-12-23; просмотров: 313; Мы поможем в написании вашей работы!; Нарушение авторских прав |