Меры вариации для сгруппированных данных. Правило сложения дисперсий

Вариация признаков, как правило, обусловлена влиянием различных факторов. Если совокупность разбить на группы по факторному признаку, то это окажет определенное влияние на значение вариации признака в группах. Выявить долю вариации, определяемую теми или иными факторами, можно разделяя всю совокупность на группы по фактору, влияние которого исследуется. Чаще всего для этих целей используются показатели вариации для сгруппированных данных. В этом случае выделяют три вида дисперсий: Общую дисперсию; внутригрупповую дисперсию, межгрупповую дисперсию.

Общая дисперсия измеряет вариацию признака во всей совокупности под влиянием всех факторов. Внутригрупповая дисперсия измеряет вариацию признака внутри группы, а межгрупповая дисперсия измеряет вариацию групповых средних относительно общей средней.

Рассмотрим простейший случай, когда исходная совокупность делится на однородных групп по одному признаку-фактору.

Допустим, имеется распределение исходной совокупности, представленное в следующей таблице:

Значение признака	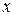Число единиц в -й группе	Итого
			…	m
			…
			…
…	…	…	…	…	…
			…
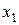
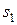
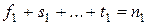
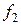
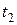
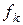
Итого			…

Сначала вычислим частных средних, то есть среднее значение признака в каждой группе:

, , .

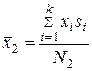На основе частных средних определяем общую среднюю по формуле

, где .

Общая дисперсия совокупности

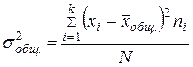
Общая дисперсия отражает вариацию признака за счет всех условий (факторов), действующих в совокупности.

Вариацию между группами за счет признака-фактора, положенного в основу группировки, отражает межгрупповая дисперсия, которая исчисляется как отклонение групповой средней от общей средней:

Вариацию внутри каждой группы изучаемой совокупности отражает частная групповая (внутригрупповая) дисперсия, которая исчисляется как средний квадрат отклонений значений признака 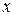от частной средней

, …

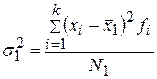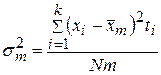
В общем виде частную (внутригрупповую) дисперсию запишем так:

, где - частоты от в каждой группе.

Так как изучаемая совокупность разбита на несколько групп, то для всей совокупности внутригрупповую вариацию будет выражать средня из внутригрупповых дисперсий, которая рассчитывается как средняя арифметическая из групповых дисперсий:

Существует закон, связывающий три вида дисперсии,

Общая дисперсия равна сумме межгрупповой дисперсии и средней из внутригрупповых дисперсий:

Логика этого закона проста: общая дисперсия, возникающая под воздействием всех факторов, формируется из дисперсии, возникающей за счет фактора группировки и дисперсии, возникающей под воздействием всех прочих факторов.

С помощью закона сложения дисперсий можно оценить удельный вес факторов, лежащих в основе группировки, во всей совокупности факторов, воздействующих на результативный признак. Для этого применяется коэффициент детерминации, который рассчитывается как отношение факторной дисперсии к общей дисперсии результативного признака:

Корень квадратный из коэффициента детерминации называют эмпирическим корреляционным отношением:

Этот показатель принимает значения в интервале [0,1]. Промежуточные значения h оцениваются по степени их близости к предельным.

Качественная оценка связи между признаками (шкала Чеддока)

	Связь		Связь
0-0,2 0,2-0,3 0,3-0,5	Отсутствует Очень слабая Слабая Умеренная	0,5-0,7 0,7-0,9 0,9-0,99	Заметная Тесная Весьма тесная Функциональная