
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
ТЕМА №5. Кореляційний аналіз
5.1. Кореляція випадкових величин та коефіцієнт кореляції
Кореляційний аналіз - сукупність методів виявлення кореляційної залежності між випадковими величинами чи ознаками.
Для числової оцінки можливого зв'язку між двома випадковими величинами: Y(із математичним очікуванням Myі середньоквадратичним відхиленнямSy) та X (із математичним очікуванням Mx і середньоквадратичним відхиленням Sx) використовується коефіцієнт кореляції:

де n - кількість спостережень,
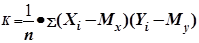 , що ґрунтується на використанні змішаного моменту між випадковими величинами Х та У.
, що ґрунтується на використанні змішаного моменту між випадковими величинами Х та У.
Цей коефіцієнт може набувати значення від -1 до +1 —залежно від тісноти зв'язку між даними випадковими величинами.
Основні властивості коефіцієнта кореляції :
1. Числове значення коефіцієнта кореляції знаходиться в межах:
-1£Rxy£1.
2. Залежність між X і Y тим сильніша, чим ½Rxy½ за модулем ближче до 1.
3. ЯкщоRxy>0, тоді зі зростанням X у середньому зростає і Y.
4. ЯкщоRxy<0, тоді при зростанні X величина Y у середньому зменшується.
5. ПриRxy=0, величини X і Y називають некорельованими ї їх можна вважати випадковими та незалежними.
6. При Rxy=1спостерігається лінійний зв'язок між X і Y (саме тому часто говорять про лінійну кореляцію).
Значення коефіцієнта парної кореляції вказує на близькість залежностей властивостей X і Y до функціональної та про ступінь інтенсивності їх зв'язку. Слабка кореляція, тобто слаба "чутливість" однієї властивості до змін іншої через її "недостатню реакцію" (тільки в середньому), зумовлює слабку "керованість" однієї властивості шляхом зміни іншої.
Нижче наведена шкала Чеддока, що використовується для оцінки тісноти зв'язку між факторами:
| Модуль коефіцієнта кореляції | Тіснота зв'язку |
| Функціональна | |
| 0,9 - 0,99 | Досить висока |
| 0,7 – 0,89 | Висока |
| 0,5 – 0,69 | Значна |
| 0,3 – 0,49 | Помірна |
| 0,1 – 0,29 | Слабка |
| Кореляційний зв'язок відсутній |
В системному аналізі доводиться вирішувати питання і про зв'язок декількох (більше за двох) випадкових величин, тобто питання про множинну кореляцію.
Нехай X, Y і Z - випадкові величини, за результатами спостереження над якими встановлено їх математичні очікування Mx, My, Mz і середньоквадратичні відхилення Sx, Sy, Sz.
Тоді можна знайти парні коефіцієнти кореляції Rxy, Rxz, Ryz за наведеною вище формулою. Але цього явно недостатньо - адже для кожного із трьох коефіцієнтів відсутні відомості про вплив третьої випадкової величини.
Якщо змінна X корелює зі змінною Y, враховуючи вплив всіх інших незалежних змінних таку кореляцію іноді називають приватною кореляцією.
Якщо одна величина корелює з іншою, то це може бути відображенням того факту, що вони обидві корелюють з третьою величиною чи із сукупністю величин.
У випадках множинного кореляційного аналізу розраховуються приватні коефіцієнти кореляції — наприклад, оцінка впливу Z на зв'язок між X і Y:
Rxy.z= 
Коефіцієнти множинної кореляції Rx.yz, Ry.zx, Rz.xy визначають який зв'язок існує між даною випадковою величиною і сукупністю інших. Формули для обчислення коефіцієнтів побудовані за тими ж принципами - урахування зв'язку однієї з величин із всіма іншими в сукупності.
5.2. Дослідження залежностей кореляції від вибору шкали вимірювання
Оскільки в аналітичному досліджені можуть бути використані різні типи шкал (номінальна, рангова, інтервальна, відносна) то виникає питання про особливості обрахування коефіцієнту кореляції при використанні даних, що виміряні за різними шкалами.
Обидві змінні виміряні за кількісними шкалами:
У цьому випадку обчислюється лінійний коефіцієнт кореляції Пірсона:  де K - кореляційний момент; Sx Sy- середні квадратичні відхилення.
де K - кореляційний момент; Sx Sy- середні квадратичні відхилення.
Одна із змінних виміряна за ранговою шкалою, а інша - за кількісною:
Припустимо, що X вимірюється в ранговій шкалі, Y - в інтервальній шкалі (або відносній). Для таких величин можна перетворити оцінки Y в ранги і знайти коефіцієнти рангової кореляції Спірмена або Кендала.
Обидві змінні вимірюються за ранговою (порядковою) шкалою:
Для таких величин вихідні дані можуть бути перетворені в ранги або просто бути рангами, при цьому обчислюються коефіцієнти рангової кореляції. Таких коефіцієнтів декілька, один з яких коефіцієнт рангової кореляції Спірмена -Rs:
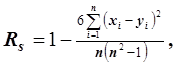 де
де
змінні X і Y набувають значення 1,2,…,n ;
n - кількість рангів;
(xi-yi)- різниця між рангом i-го об'єкта по X і його ж рангом по Y.
Коефіцієнти рангової кореляції вимірюють тісноту зв'язку між величинами, які можна розташувати за зростанням чи зниженням ступеня інтенсивності кожної. Така процедура має назву ранжування ряду.
Ряд величин можна ранжувати за двома і більше властивостями. І якщо існує тенденція одночасного збільшення (зменшення) двох властивостей, то це означає, що між цими властивостями існує зв'язок.
При наявності n послідовних і необ'єднаних рангів 1,2,…,n, використовується коефіцієнт рангової кореляції Кендала:

де S = P-Q, 
Р - кількість пар рангів з прямим порядком;
Q - кількість пар рангів з зворотним порядком;
n - загальна кількість рангів.
При t=+1 всі пари рангів мають прямий порядок; при t=-1 всі пари мають зворотний порядок рангів; при t=0 кількість пар з прямим і зворотним порядками рангів однакова.
Також для обчислення коефіцієнта рангової кореляції t можна використовувати способи, що не потребують складання таблиці, кількості пар рангів. Для цього формула tперетворюється так, щоб вона містила або кількість пар рангів з прямим порядком Р, або зі зворотним порядком Q:

Відмінність між цими коефіцієнтами полягає в тому, що при визначенні коефіцієнта рангової кореляції Кендела tфіксується тільки факт прямого або зворотного розташування рангів для кожної пари елементів, незалежно від віддалення рангів один від одного.
Одна із змінних вимірюється за номінальною, а інша - за кількісною шкалою:
Для таких величин визначення зв'язку між X і Y зручно використовувати наступну формулу:
 , де
, де
x1 - середнє відхилення по X об'єктів, що мають одиниці по Y;
x0- середнє відхилення по X об'єктів, що мають нулі по Y;
dx - стандартне відхилення n значень по X;
n1- число об'єктів, що мають одиницю по Y;
n2- число об'єктів, що мають нуль по Y.
Обидві змінні вимірюються за номінальною шкалою:
Для таких величин коефіцієнт кореляції можна обчислити за формулою:  , де
, де
px - частка об'єктів, що мають одиницю по X ;
qx - частка об'єктів, що мають нуль по X;
py - частка об'єктів, що мають одиницю по Y;
qy - частка об'єктів, що мають нуль по Y;
pxy - частка об'єктів, що мають одиницю по X і по Y одночасно.
Питання для самоконтролю
1. Охарактеризувати типи шкал, що використовуються для вимірювання випадкових величин в системі.
2. Охарактеризувати основні етапи кореляційного аналізу.
3. Охарактеризувати коефіцієнт кореляції та його показники.
4. Охарактеризувати поняття множинної кореляції.
5. Охарактеризувати поняття приватної кореляції.
6. Визначити коефіцієнт кореляції, що використовується для номінальних величин.
7. Визначити коефіцієнт кореляції, що використовується для комбінації номінальної та кількісної шкал.
8. Визначити для яких величин застосовується коефіцієнт кореляції Спірмена.
9. Визначити для яких величин застосовується коефіцієнт кореляції Кендела.
10. Визначити для яких величин застосовується коефіцієнт кореляції Пірсона.
Типовий приклад
Мета дослідження: Ознайомитись з базовими поняттями кореляції випадкових величин. Оволодіти навичками кореляційного аналізу та дослідження залежностей кореляції від вибору шкали вимірювання.
Задача дослідження: провести змістовний аналіз досліджуваної системи за наступним планом:
1. Встановити причинно-наслідкові зв’язки між елементами системи.
2. Використовуючи методи кореляційного аналізу перевірити наявність та силу зв’язку між величинами, що вимірюються за разними типами шкал.
Рішення задачі:
1. Обидві змінні виміряні за кількісними шкалами (коефіцієнт кореляції Пірсона):
За результатами проведеного аналітичного дослідження були отримані кількісні показники властивостей двох величин X таУ, при 15 спостереженнях. Потрібно підтвердити чи спростувати гіпотезу про існування кореляційного зв’язку між X таУ. Результати спостереження занесені до таблиці:
| № | Х | У |
| 12.25 | ||
| 11.96 | ||
| 10.74 | ||
| 9.9 | ||
| 11.85 | ||
| 9.35 | ||
| 9.26 | ||
| 9.83 | ||
| 9.1 | ||
| 9.26 | ||
| 8.7 | ||
| 9.27 | ||
| 9.77 | ||
| 7.8 | ||
| 8.06 |
За нульову гіпотезу приймається: Њ0 ="існує позитивний зв’язок" , як альтернативна: Њ1="зв’язку немає".
Властивість Xта Увизначаються за інтервальною (кількісною) шкалою відповідно приймають природні значення.
За даними таблиці:

де K - кореляційний момент, Sx Sy- середні квадратичні відхилення.
Гіпотеза Њ0 підтвердилась: між величинами X і Y існує сильний позитивний зв’язок (при збільшення X значення Y також збільшується).
2.Обидві змінні вимірюються за ранговою шкалою (коефіцієнт рангової кореляції Спірмена):
За результатами проведеного аналітичного дослідження були отримані кількісні показники властивостей двох величин X таУ при 15 спостереженнях. Потрібно підтвердити чи спростувати гіпотезу про існування кореляційного зв’язку між X таУ.
За нульову гіпотезу приймається: Њ0 ="існує позитивний зв’язок", як альтернативна: Њ1="зв’язку немає".
Властивості величин Xта Увизначається за ранговою шкалою, відповідно Xi та yi набувають значення від 1 до 15.
Розподіл випадкових величин Xта У поданий у вигляді таблиці:
| № | РАНГ Х | РАНГ У |
За даними таблиці:
n =15 (кількість рангів);
n(n2-1)=3360
(Xi-Yi)2 = 83 (квадрат різниці між рангом i-го об'єкта по X і його ж рангом по Y).
 =0.85
=0.85
Гіпотеза Њ0 підтвердилась: між величинами X і Y існує сильний позитивний зв’язок (при збільшення X значення Y також збільшується).
3.Обидві змінні вимірюються за ранговою шкалою (коефіцієнт рангової кореляції Кендала):
За результатами проведеного аналітичного дослідження були отримані кількісні показники властивостей двох величин X таУ при 10 спостереженнях. Потрібно підтвердити чи спростувати гіпотезу про існування кореляційного зв’язку між X таУ.
Властивості величин Xта Увизначається за ранговою шкалою, відповідно Xi та yi набувають значень від 1 до 10. Для зручності обробки результатів, кожному із спостережень надане ім’я, що відповідає літері латинського алфавіту. Розподіл випадкових величин Xта У поданий у вигляді таблиці:
| НАЗВА спостереження | РАНГ Х | РАНГ У |
| A | ||
| B | ||
| C | ||
| D | ||
| E | ||
| F | ||
| G | ||
| H | ||
| I | ||
| J |
З порівняння рядів випливає, що існує певний зв'язок між Х та У, оскільки виявляється тенденція до скупчення менших значень рангів на початку і великих значень рангів наприкінці третього стовпчика (У). Отже, порядок розташування рангів по Х відносно рангів по У визначає ступінь їх взаємозалежності. Ступінь безладу визначається кількістю пар по У, розташованих у зворотному порядку (B і C- 4 і 3; E і F - 7 і 6; ...), оскільки саме така кількість операцій потрібна для зворотної перестановки елементів у парах, щоб перетворити ряд У на впорядкований.
Метод №1: визначимо всі можливі пари рангів, кожній парі з прямим порядком елементів присвоїмо значення "+", а із зворотним - значення "-". Дані представлені у вигляді таблиці:
| Пара рангів | Порядок рангів | Пара рангів | Порядок рангів | Пара рангів | Порядок рангів | Пара рангів | Порядок рангів |
| AB | + | BF | + | DE | + | FH | + |
| AC | + | BG | + | DF | + | FI | + |
| AD | + | BH | + | DG | + | FJ | + |
| AE | + | BI | + | DH | + | GH | + |
| AF | + | BJ | + | DI | + | GI | + |
| AG | + | CD | + | DJ | + | GJ | + |
| AH | + | CE | + | EF | - | HI | + |
| AI | + | CF | + | EG | - | HJ | - |
| AJ | + | CG | + | EH | + | IJ | - |
| BC | - | CH | + | EI | + | ||
| BD | - | CI | + | EJ | + | ||
| BE | + | CJ | + | FG | - |
За даними таблиці:
Р = 38 (кількість пар рангів з прямим порядком);
Q = 7 (кількість пар рангів з зворотним порядком);
n =10 (загальна кількість рангів);
S = P-Q= 31
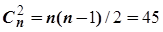
 =0.69
=0.69
Гіпотеза Њ0 підтвердилась: між величинами X і Y існує сильний позитивний зв’язок (при збільшення X значення Y також збільшується).
Метод №2: для визначення Р треба підрахувати кількість пар рангів по ряду У={1, 4, 2, 3, 7, 6, 5, 9, 10, 8}, що мають прямий зв’язок. Так для першого елементу ряду "1", прямий порядок утворюють всі дев’ять елементів, що знаходяться праворуч від нього. Для "1" таких елементів - 9, для "4" таких елементів - 6, для "2" таких елементів - 7, для "3" таких елементів - 6, для "7" таких елементів - 3, для "6" таких елементів - 3, для "5" таких елементів - 3, для "9" таких елементів - 1, для "10" таких елементів - 0, відповідно Р=9+6+7+6+3+3+3+1+0=38і
 =0.69
=0.69
Для порівняння: коефіцієнт рангової кореляції Спірмена для даного прикладу дорівнює Rs=0.88.
4. Одна із змінних вимірюється за номінальною, а інша - за кількісною шкалою:
За результатами проведеного аналітичного дослідження були отримані кількісні показники властивостей двох величин X таУ, при 15 спостереженнях. Потрібно підтвердити чи спростувати гіпотезу про існування кореляційного зв’язку між X таУ. Результати спостереження занесені до таблиці:
| № | Х | У |
За нульову гіпотезу приймається: Њ0 ="існує позитивний зв’язок" , як альтернативна: Њ1="зв’язку немає".
Властивість Xвизначається за інтервальною (кількісною) шкалою, відповідно X i приймає природні значення.
Властивість Увизначається за номінальною шкалою з варіантами відповідей "Так" і "Ні", відповідно yi приймає значення 1 та 0.
За даними таблиці:
 =0.87, де
=0.87, де
x1 - середнє відхилення по X об'єктів, що мають одиниці по Y;
x0- середнє відхилення по X об'єктів, що мають нулі по Y;
dx - стандартне відхилення n значень по X;
n1- число об'єктів, що мають одиницю по Y;
n2- число об'єктів, що мають нуль по Y.
Гіпотеза Њ0 підтвердилась: між величинами X і Y існує сильний позитивний зв’язок (при збільшення X значення Y також збільшується).
5.Обидві змінні вимірюються за номінальною шкалою:
За результатами проведеного аналітичного дослідження були отримані кількісні показники властивостей двох величин X таУ при 15 спостереженнях. Потрібно підтвердити чи спростувати гіпотезу про існування кореляційного зв’язку між X таУ. Дані спостереження занесені в таблицю:
| № | Х | У |
| ТАК | ТАК | |
| ТАК | ТАК | |
| ТАК | ТАК | |
| ТАК | ТАК | |
| ТАК | ТАК | |
| ТАК | ТАК | |
| НІ | ТАК | |
| НІ | ТАК | |
| НІ | НІ | |
| НІ | НІ | |
| НІ | НІ | |
| НІ | НІ | |
| НІ | НІ | |
| НІ | НІ | |
| НІ | НІ |
За нульову гіпотезу приймається: Њ0 ="існує позитивний зв’язок", як альтернативна: Њ1="зв’язку немає".
Властивості величин Xта Увизначається за номінальною шкалою з варіантами відповідей "Так" і "Ні", відповідно X i та yi набувають значення 1 та 0.
Розподіл випадкових величин Xта У поданий у вигляді таблиці:
| № | Х | У |
За даними таблиці:
px = 6/15=0,4 (частка об'єктів, що мають одиницю по X);
qx = 9/15=0,6 (частка об'єктів, що мають нуль по X);
py = 8/15=0,53 (частка об'єктів, що мають одиницю по Y);
qy = 7/15=0,47 (частка об'єктів, що мають нуль по Y);
pxy =6/15=0,4 (частка об'єктів, що мають одиницю по X і по Y одночасно);
 =0.76
=0.76
Гіпотеза Њ0 підтвердилась: між величинами X і Y існує сильний позитивний зв’язок (при збільшенні X значення Y також збільшується).
Індивідуальне завдання
Використовуючи основні процедури та методи системного аналізу продовжити самостійне дослідження системи, що була обрана для дослідження (індивідуальне завдання Тема №1) за наступним планом:
1. Встановити причинно-наслідкові зв’язки між елементами системи.
2. Використовуючи методи кореляційного аналізу перевірити наявність та силу зв’язку між досліджуваними величинами (за схемою типового прикладу).
Поради до виконання індивідуального завдання
Для того, щоб визначитись які із змінних системи обрати для кореляційного проведіть змістовний аналіз причинно-наслідкових зв’язків між показниками системи. Виберіть дві залежні (чи не залежні) змінні які мають природні кількісні розмірності та знайдіть відповідні статистичні дані про них. Висуньте нульову гіпотезу, що до їх кореляційної залежності. Перевірте гіпотезу за наступною схемою:
1. Розрахуйте для них коефіцієнт кореляції Пірсона.
2. Оцініть значення цих змінних за ранговою шкалою та порахуйте по черзі коефіцієнт рангової кореляції Спірмена та Кендала.
3. Поверніться до кількісного значення однієї з величини, а іншу оцініть за номінальною шкалою та порахуйте коефіцієнт кореляції за відповідною формулою.
4. Оцініть за номінальною шкалою обидві змінні та порахуйте коефіцієнт кореляції за відповідною формулою.
У висновку дайте змістовний аналіз кількісним значенням отриманих коефіцієнтів.
Теми для обговорення
1. Кореляційний зв’язок параметрів системи міжнародних відносин.
2. Кореляційна матриця та методи її аналізу.
3. Змістовні обмеження на застосування кореляційного аналізу.
Зразок тестових завдань
1. Які з наступних стверджень вірні:
a) При Rxy=1 спостерігається лінійний зв'язок між X і Y
b) Якщо Rxy³0, тоді зі зростанням X у середньому зростає і Y
c) При Rxy= -1 кореляційний зв'язок між X і Y відсутній
2. Для якісної оцінки взаємозв'язку випадкових величин застосовують:
a) когнітивні моделі
b) морфологічні моделі
c) кореляційний аналіз
3. Коефіцієнт парної кореляції між Х та У = 0,8. Коефіцієнт парної кореляції між Х та Z = - 0,8.
a) величини У та Z однаково впливають на Х
b) величина У сильніше впливає на Х чим Z
c) сила кореляційного зв’язку однакова
Основна література
1. Сізих Н.В. Теорія прийняття рішень в міжнародних відносинах: Навчальний посібник для лекційного курсу. - К.: Кобза, 2003. - 208 с.
2. Циба В.Т. Математичні основи соціальних досліджень: кваліметричний підхід. - К.:МАУП, 2002. - 248 с.
3. Международные отношения: социологические подходы / под ред. П.А. Цыганкова. – М., 2006. – 346 с.
4. Лигун А. А., Малышева А. Д. Математическая обработка результатов эксперимента. Днепродзержинск: ДИИ, 1992—47с.
5. Саати Т. Математические модели конфликтных ситуаций — М.: Сов. радио, 1989. — 304 с.
Дата добавления: 2014-12-30; просмотров: 645; Мы поможем в написании вашей работы!; Нарушение авторских прав |