
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Кількісні шкали: Int. інтервальна шкала; Rel. відносна шкала.
Ці дві шкали застосовується до тих величин, що мають натуральні розмірності. Для таких величин припустимі всі арифметичні дії. Якщо деяка величина може приймати на кількісній шкалі значення X, Y чи Z, то справедливими вважаються вирази типу:
(X¹Y), (X=Z), (X<Y), (Y>Z), (Z£X), (Z³Y), (X+Y), (Z-X), (Y·Z), (Z¸X).
Різниця між інтервальною та відносною шкалою:
Схематично інтервальна шкала виглядає: 0_______________+¥,
а відносна: -¥_______________0_______________+¥,
Відповідно до схеми інтервальна шкала не має від’ємних значень, а 0 (нуль) на інтервальній шкалі означає відсутність значення.
3.9. Поняття статистичної гіпотези
Статистичних гіпотез завжди дві і вони взаємовиключні. Одну з них називають нульовою гіпотезою Њ0, а другу – альтернативною гіпотезою Њ1,що завжди протилежна нульовій.
Для процедури перевірки статистичних гіпотез існує поняття рівня значимості результатів спостережень. Теорія ймовірностей розділяє події на три класи: звичайні, рідкісні і виняткові. При цьому спостереження виняткової події дає підстави вважати, що причина його настання невипадкова, бо має місце впливу деякого фактора.
Метод виділення рідкісних подій пропонує вважати подію рідкою, якщо її імовірність не перевищує 5% таке значення є умовним і залежить від поставленої задачі. У деяких випадках рідкими вважають події з імовірністю не більш 1%, хоча саме використання п’яти відсоткового рівня значимості прийнято майже у всіх прикладних напрямках статистики, у тому числі й в економіці.
Якщо спостереження відносяться до рідких подій (з імовірністю до 5%), то такі спостереження і результати їхньої обробки називають статистично значимими. Якщо імовірність деякого результату спостереження в умовах основної гіпотези виявиться дуже малою, то чим вона менше, тим більше підстав відхилити Њ0. З іншого боку, якщо відбудеться дуже рідкісна подія то значимість такого спостереження надзвичайно висока.
Статистичний критерій - правило відповідно якого приймається чи відхиляється та чи інша гіпотеза.
На жаль, не існує єдиного, універсального критерію значимості – їх доводиться розробляти в теорії і використовувати на практиці відповідно до особливостей конкретних задач.
3.10. Метод перевірки узгодженості думок експертів
Випадкові величини, що вимірюються за ранговою шкалою Ord, як правило мають більше ніж два припустимих значення, тобто припускається наявність декількох фіксованих значень, упорядкованих за деякою ознакою, чи властивості. У цих випадках говорять, що випадкова величина може бути величиною “першого рангу”, “другого рангу” і т.п.
Існують і різні, обґрунтовані й апробовані методи аналізу таких величин. Відмінність між ними полягає лише у способі розрахунку критерію, прийнятті чи відкиданні нульової гіпотези.
Один з таких методів, що найчастіше використовується для аналізу експертних оцінок, запропоновано М. Кендаллом і має назву "показник погодженості рангів" чи коефіцієнт конкордації:
W = S / Smax, де S- сума квадратів відхилень;
Smax= m2 · (n3– n) / 12, де
m - кількість експертів; n - кількість факторів;
Числове значення коефіцієнта конкордації знаходиться в межах 0£W£1. При W=1спостерігається максимальна погодженість, приW=0 погодженості немає.
Питання для самоконтролю
1. Класифікувати випадкові події. Навести приклади.
2. Охарактеризувати поняття імовірність випадкової події. Навести приклад.
3. Проаналізувати методи розрахунку імовірності випадкових подій.
4. Порівняти поняття залежність та сумісність подій. Навести приклад.
5. Охарактеризувати поняття повна імовірність подій. Навести приклад.
6. Охарактеризувати основні кількісні показники соціальних систем.
7. Визначити суть основної та альтернативної гіпотез дослідження.
8. Визначити алгоритм остаточного вибору робочої гіпотези.
9. Проаналізувати принципи виділення рідких подій.
10. Проаналізувати метод перевірки статистичної гіпотези за допомогою використання коефіцієнта конкордації.
Типовий приклад
Мета дослідження: ознайомитись з базовими поняттями перевірки статистичної гіпотези. Оволодіти навичками використання коефіцієнта конкордації для перевірки статистичної гіпотези в галузях міжнародних відносин.
Задача дослідження: провести змістовний аналіз досліджуваної системи за наступним планом:
1. Розробити анкети для визначення ефективності впливу факторів на систему та провести анкетування.
2. Обробити результати анкетування.
3. Обрахувати коефіцієнт узгодженості та зробити висновки.
Рішення задачі:
1. Анкета:
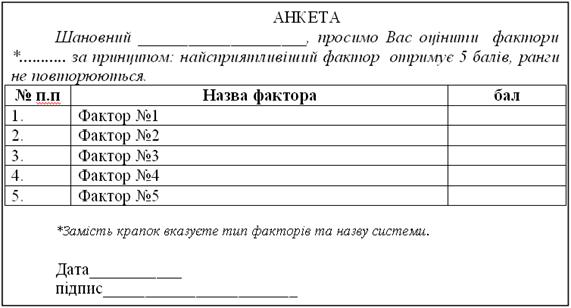
2. Опитування:
Далі дванадцять експертів (замість прізвищ експертів використовуються перші 12 літер латинського алфавіту) ранжують шість факторів (F1, F2, F3, F4, F5, F6), що впливають на ефективність системи, за принципом: найсприятливіший фактор дорівнює 6, ранги не повторюються. За нульову гіпотезу приймається: Њ0 ="думки експертів погоджені", як альтернативна: Њ1="думки експертів суттєво різняться".
3. Обробка результатів:
Дані спостережень занесені в таблицю:
| Фактори | F1 | F2 | F3 | F4 | F5 | F6 | СУМА |
| Експерти | |||||||
| A | |||||||
| B | |||||||
| C | |||||||
| D | |||||||
| E | |||||||
| F | |||||||
| G | |||||||
| H | |||||||
| I | |||||||
| J | |||||||
| K | |||||||
| M | |||||||
| Сума рангів | |||||||
| Сумарний ранг | |||||||
| Відхилення суми рангів від D=42 | -26 | -15 | -6 | ||||
| Квадрати відхилень |
За даними таблиці: повна сума рангів складає 252, що дає D=252/6=42 на фактор. Для кожного з факторів спостерігається відхилення суми рангів, зазначених експертами, від середнього значення. Для загального випадку при n факторів і m експертів середнє значення суми рангів для будь-якого фактора визначиться формулою: D =0.5·m·(n+1).
Оскільки сума цих відхилень завжди дорівнює нулю, для їхнього усереднення використовують квадрати їх значень.
S =1786, Smax=m2 · (n3– n) / 12= 122 · (63– 6) / 12=2520
W = S / Smax =1786/2520=0.71
4. Висновки:
Значення коефіцієнта конкордації для даного прикладу складає близько 0.8, а цього більш ніж достатньо для прийняття Њ0 гіпотези про погодженість думок експертів, що найвпливовішим виявився 1 фактор.
Індивідуальне завдання
Використовуючи основні процедури та методи системного аналізу продовжити самостійне дослідження системи, що була обрана для аналізу (індивідуальне завдання Тема №1) за наступним планом:
1. Розробити анкети для визначення ефективності запропонованої системи та провести анкетування (мінімальна кількість факторів-5, мінімальна кількість експертів-10).
2. Обробити результати анкетування за схемою типового прикладу.
3. Обрахувати коефіцієнт узгодженості та зробити висновки.
Поради до виконання індивідуального завдання
Основна задача цього дослідження - оцінити за силою впливу фактори, що були обрані для попереднього когнітивного аналізу (індивідуальне завдання Тема №2). Інструментом такої оцінки стають рішення експертів.
На результати експертного оцінювання впливають різні фактори, серед яких і якість розробленої Вами анкети. ЇЇ требо розробити таким чином, щоб запитання були зрозумілі та однозначні.
Запропонуйте заповнити анкету фахівцям в даної галузі дослідження, запам'ятайте - експертів повинно бути суттєво більше ніж факторів, а їх компетентність першочергово впиває на узгодженість рішень.
Обробіть отримані результати, якщо рішення експертів виявиться неузгодженим, спробуйте збільшити кількість експертів чи перевірити їх компетентність.
Висуньте власну гіпотезу, що до рангів факторів, а у висновку порівняйте власну апріорну гіпотезу з рішенням експертів.
Теми для обговорення
1. Проблеми недоступності знань в соціальних системах.
2. Порівняльний аналіз методів визначення імовірності випадкової величини
3. Якісний та кількісний аналіз змінних системи.
Зразок тестових завдань
1. Яка з наведених величин дискретна:
a) площа країни
b) температура повітря
c) рейтинг країни
2. Яку величину можна вимірювати лише за номінальною шкалою:
a) кількість законодавчих актів
b) партійну приналежність
c) наявність політичних уподобань
3. По запропонованим даним заповніть таблицю до кінця:
| Експерти | F1 | F2 | F3 | S |
| Фактори | ||||
| A | ||||
| B | ||||
| C | ||||
| D | ||||
| Сума рангів | ||||
| Сумарний ранг | ||||
| Відхилення від середнього | ||||
| Квадрати відхилень |
Основна література
1. Картенко А.В. Системний аналіз об'єктів та процесів комп'ютеризації: Навчальний посібник. - Львів: "Новий світ-2000" , 2003. - 424 с.
2. Грехем Р., Кнут Д., Паташник О. Конкретная математика. Основание информатики. - М.: Мир, 1998. - 703 с.
3. Международные отношения: социологические подходы / под ред. П.А. Цыганкова. – М., 2006. – 346 с.
4. Лигун А. А., Малышева А. Д. Математическая обработка результатов эксперимента. Днепродзержинск: ДИИ, 1992—47с.
5. Саати Т. Математические модели конфликтных ситуаций — М.: Сов. радио, 1989. — 304 с.
Дата добавления: 2014-12-30; просмотров: 516; Мы поможем в написании вашей работы!; Нарушение авторских прав |