
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Статистичні.
Функціональні залежності спостерігаються тоді, коли одній властивості випадкової величини однозначно відповідає одне або кілька значень іншої. Функціональна залежність двох кількісних змінних полягає в тому, що кожному значенню однієї змінної завжди відповідає визначене значення іншої змінної.
Статистичні залежності спостерігаються тоді, коли одній властивості випадкової величини відповідає множина значень іншої властивості у вигляді статистичного розподілу. На відміну від функціональної залежності, коли кожному значенню однієї ознаки завжди відповідає визначене значення іншої, при статистичній залежності тому самому значенню однієї ознаки можуть відповідати різні значення іншої.
Якщо виявлено, що кожного разу коли змінюється величина A змінюється і величина B, то можна зробити висновок: "величина A впливає на величина B", тобто між змінними А та В є причинна залежність. Змінні величини залежні, якщо у наявних спостереженнях їх значення систематично погоджені.
Можна відзначити дві найпростіші властивості взаємозалежності між змінними величинами:
- величинавзаємозалежності;
- надійністьвзаємозалежності.
Поняття залежності і надійності представляють дві різні характеристики зв’язку між змінними. Проте, не можна сказати, що вони зовсім незалежні. Чим більша залежність між величинами, тим вона надійніша.
4.2. Аналіз взаємної спряженості випадкових величин
В якості числової характеристики, що визначає взаємний вплив випадкових величин можуть використовуватися коефіцієнти взаємної спряженості. В основі коефіцієнтів взаємної спряженості лежить показник спряження c2 між розподілами двох властивостей, тобто визначення ступеня збіжності (спряженості) емпіричних умовних розподілів випадкових величин (X½У) при різних значеннях Yj з безумовним розподілом випадкової величини X за формулою:
 , де
, де
WH - теоретична відносна частота, WE - експериментальна відносна частота, k - кількість інтервалів на шкалі.
Чисельник формули виражає різницю між частотами теоретичного й емпіричного розподілів кожного доданка, піднесену до квадрата; дріб визначає відносну частку розбіжності для кожного доданка; сума виражає загальну відносну розбіжність емпіричного й теоретичного розподілів.
Отримане значення c2називають емпіричним, тобто отриманим експериментальним шляхом. Існують статистичні таблиці (Додаток 1) функції F(c2) з розрахованими критичними значеннями c2 для різних рівнів значимості та числа ступенів свободи v=(k-1). Саме різниця між емпіричним значенням c2е та табличним критичним значенням c2кр впливає на прийняття (відхилення) гіпотези.
Якщо емпіричний і теоретичний розподіли випадкової величини збігаються, то різниці між відповідними частотами дорівнюють нулюі c2 =0. Чим більші ці різниці, тим більше емпіричний розподіл не збігається з теоретичним законом.
Ця випадкова величина була запропонована видатним статистиком Р.Фішером для перевірки гіпотез що до відповідність вибіркового розподілу деякому заданому закону.
4.3. Коефіцієнти Пірсона та Чупрова
Сам по собі c2 залежить від n і не є нормованою величиною тісноти зв'язку. Коефіцієнт зв'язку між властивостями не повинен залежати від кількості спостережень і має перебувати в межах від нуля до одиниці. Кількісними показниками спряженості величин є два коефіцієнти взаємної спряженості:
коефіцієнт Пірсона: 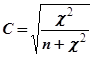
коефіцієнт Чупрова: 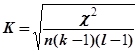
де (k - 1)(l - 1) = v - число ступенів свободи.
Мінімальне значення кожного з цих коефіцієнтів дорівнює нулю. Результат c2 дорівнює 0, виражає факт незалежності Х від У.
Максимальне значення кожного з цих коефіцієнтів дорівнює одиниці. Результат c2 дорівнює знаменнику, виражає факт сильної залежності Х від У.
Хоча коефіцієнти Пірсона і Чупрова відображають одне й те саме явище, вони не рівні у загальному випадку. В загальному випадку коефіцієнт Пірсона перевищує коефіцієнт Чупрова в квадратний корінь з числа ступенів свободи:

4.4. Коефіцієнт контингенції та асоціації
Формулу для обчислення коефіцієнта взаємної спряженості Чупрова використовують також для визначення зв'язку, коли обидві змінні вимірюються за номінальною шкалою. Традиційний підхід до аналізу зв'язку між номінальними ознаками базуються на перевірці припущення про статистичну незалежність розглянутих ознак у випадкових величин.
Спільний розподіл двох таких величин Х та У наведено в таблиці:
| Х | "НІ" | "ТАК" | СУМА |
| У | |||
| "НІ" | a | b | a+b |
| "ТАК" | c | d | c+d |
| СУМА | a+c | b+d | n |
Якщо обидві змінні вимірюються за номінальною шкалою, кількість інтервалів на шкалі для них k=l=2 (існує тільки два значення "ТАК", "НІ"), відповідно число ступенів свободи v=(k-1)(l-1)=(2-1)(2-1)=1.
Коефіцієнт взаємної спряженості для двох змінних, які вимірюються за номінальною шкалою, називається коефіцієнтом контингенції та розраховується за формулою:

Для оцінки ступеня зв'язку між двома змінними, що вимірюються за номінальною шкалою, крім коефіцієнта контингенції, можна використовувати коефіцієнт асоціації:

Обидва коефіцієнти Φ і Q можуть набувати значення від -1 до +1 і дорівнюють 0, якщо величини статистично незалежні.
Коефіцієнт Φ приймає значення + 1, якщо b=0 і с=0. Значення -1 коефіцієнт Φ приймає у випадку, коли а=0 і d=0.
Коефіцієнт Q набуває значення +1 у випадку повного позитивного зв’язку, тобто коли c=0 чи b=0. Значення -1 коефіцієнт Q набуває у випадку повної негативної зв'язаності, коли а=0 чи d=0.
Коефіцієнт контингенції завжди менший за коефіцієнт асоціації. Зв’язок між величинами вважається підтвердженим, якщо Q³0.5 чи Φ ³0.3.
Самий точний прогноз досягається в ситуації, коли для кожного із значень однієї ознаки можна однозначно визначити відповідне значення іншої. Таким чином, сучасне трактування поняття "повний зв'язок" між величинами Х і Y означає, що знання значення Х усуває будь яку невизначеність у прогнозуванні значення Y. Для зменшення невизначеності необхідно збільшити кількість інформації про систему.
Питання для самоконтролю
1. Охарактеризувати залежності та взаємозв'язок випадкових подій в системі.
2. Порівняти функціональну та статистичну залежність.
3. Визначити властивості взаємозалежності.
4. Проаналізувати величину "хі-квадрат", як показник спряження величин в системі.
5. Проаналізувати коефіцієнт Пірсона, як кількісний показник спряження величин в системі.
6. Проаналізувати коефіцієнт Чупрова, як кількісний показник спряження величин в системі.
7. Порівняти коефіцієнт Чупрова та коефіцієнт Пірсона.
8. Проаналізувати коефіцієнт контингенції, як кількісний показник спряження величин в системі.
9. Проаналізувати коефіцієнт асоціації, як кількісний показник спряження величин в системі.
10. Порівняти коефіцієнт контингенції та коефіцієнт асоціації.
Типовий приклад
Мета дослідження: Ознайомитись з базовими поняттями взаємозалежності випадкових величин в системі. Оволодіти навичками застосування методів перевірки наявності зв’язку між величинами в системі міжнародних відносин. Навчитись використовувати в дослідженнях коефіцієнти Пірсона, Чупрова, контингенції, асоціації.
Задача дослідження: провести змістовний аналіз досліджуваної системи за наступним планом:
1. Перевірити наявність та силу зв’язку між досліджуваними величинами, використовуючи коефіцієнт Пірсона та Чупрова.
2. Перевірити наявність та силу зв’язку між досліджуваними величинами, використовуючи коефіцієнт контингенції та асоціації.
Рішення задачі:
Дата добавления: 2014-12-30; просмотров: 480; Мы поможем в написании вашей работы!; Нарушение авторских прав |