
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
ТЕМА №6. Регресійний та факторний аналіз
6.1. Метод лінійного регресійного аналізу
При вивченні імовірнісних залежностей використовується один із найбільш поширених методів опрацювання даних - метод регресійного аналізу. Він складається з визначення загального вигляду рівняння регресії, побудові статистичних оцінок невідомих параметрів, що входять у рівняння регресіїі перевірці статистичних гіпотез про регресію.
Відмінною особливістю рівнянь, які використовуються у цьому випадку, є наявність двох видів змінних - залежних і незалежних. На практиці часто використовують моделі, у яких є одна залежна змінна - функція і декілька незалежних змінних аргументів:
Y=F(X1,...Xi)
Поділ змінних на залежну і незалежні в регресійному аналізі завжди проводиться на основі змістовних понять.
У найпростішому випадку є одна залежна й одна незалежна змінна, множинна регресія має декілька незалежних змінних (регресорів). Загальна обчислювальна задача, яку вирішують при аналізі методом множинної регресії, складається в наближені прямої лінії до деякого набору крапок.
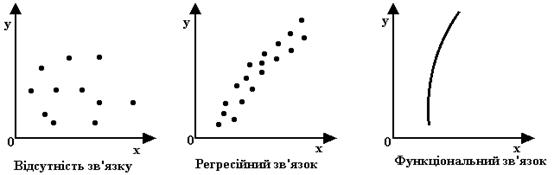 |
Лінія регресії будується так, щоб мінімізувати квадрати відхилень цієї лінії від крапок, тому цю процедуру іноді називають оцінюванням по методу найменших квадратів.

Пряма лінія на площині (у просторі двох вимірів) задається рівнянням:
Y=a·X +b.
де змінна Y може бути виражена через кутовий коефіцієнт a помножений на змінну X плюс константа b. Кутовий коефіцієнт a називають регресійним коефіцієнтом, а константу b - вільним членом.
Висувається наступна гіпотеза: випадкова величина Y при фіксованому значенні величини X розподілена нормально з математичним очікуванням
My = a· X + b і дисперсією Dy, що не залежить від X.
При наявності результатів спостережень над парами Xi і Yi попередньо обчислюються середні значення My і Mx, а потім вираховується оцінка регресійного коефіцієнта a:
Де
Rxy - коефіцієнт кореляції
Sy, Sx- середньоквадратичні відхилення по X та Y, відповідно.
За отриманим регресійним коефіцієнтом a вираховується оцінка вільного члена b:
b = My - a•MX
та проводиться перевірка значимості отриманих результатів.
Регресійний коефіцієнт a та вільний член b можна знайти і не обраховуючи математичне очікування, середньоквадратичне відхилення та коефіцієнт кореляції. Для цього застосовуються формули:


Основне концептуальне обмеження всіх методів регресійного аналізу полягає в тому, що вони дозволяють знайти тільки числові залежності, а не причинні зв'язки.
6.2. Загальна характеристика факторного аналізу
Функціонування будь-якої відкритої системи відбувається в умовах складної взаємодії комплексу внутрішніх і зовнішніх факторів.
Методи факторного аналізу дозволяють встановлювати причинно-наслідкові зв'язки, давати їм кількісну характеристику і вимірювати вплив факторів на функціонування системи.
Досліджувані в системному аналізі фактори можуть бути класифіковані за різними ознаками:
- за природою походження;
- за ступенем впливу на систему (основні і другорядні);
- за відношенням до навколишнього середовища (внутрішні і зовнішні);
- за поширеністю (загальні і специфічні);
- за часом впливу на систему (постійні і перемінні);
- за характером дії (інтенсивні і екстенсивні);
- за структурою (прості і складні);
- за рівнем ієрархії.
Крім цього фактори підрозділяються на об'єктивні, що не залежать від волі і бажань людей та суб'єктивні, що піддаються впливу діяльності юридичних і фізичних осіб.
Кількісна характеристика взаємозалежних явищ здійснюється за допомогою показників. Показники, що характеризують причину, називаються факторними (незалежними); показники, що характеризують наслідок, називаються результативними (залежними).
Для систематизації факторів створюються спеціальні факторні системи.
Факторна система - сукупність факторних і результативних ознак, зв'язаних причинно-наслідковим зв'язком.
Модель факторної системи - це математична формула, що виражає реальні зв'язки між аналізованими явищами. У загальному вигляді вона може бути представлена як:
У=F(X1, X2,...,Xn), де У - результативна ознака; Хі- факторні ознаки.
В основі факторного аналізу лежить виявлення, оцінка і прогнозування впливу факторів на зміну результативного показника.
У загальному випадку можна виділити наступні основні етапи факторного аналізу:
1. Постановка мети аналізу.
2. Добір факторів, що визначають досліджувані результативні показники.
3. Класифікація і систематизація факторів з метою забезпечення комплексного і системного підходу до дослідження їхнього впливу на систему.
4. Визначення форми залежності між факторами і результативним показником.
5. Моделювання взаємозв'язків між результативним і факторним показниками.
6. Розрахунок впливу факторів і оцінка ролі кожного з них у зміні величини результативного показника.
7. Робота з факторною моделлю (практичне її використання для керування процесами в системі).
Набір методів факторного аналізу достатньо великий та нараховує десятки різних підходів і прийомів обробки даних. До методів факторного аналізу відносять:
- центроідний метод Л. Терстоуна;
- однофакторну модель Ч. Спірмена;
- біфакторну модель Г. Хользінгера;
- груповий метод Л. Гуттмана і П. Хорста;
- метод головних факторів Г. Томсона;
- метод максимальної правдоподібності Д. Лоулі;
- мінімальних залишків Г. Хармана;
- канонічного факторного аналізу К. Рао та ін.
За допомогою факторного аналізу в конкретному дослідженні вирішуються наступні задачі:
1. Зменшення розмірності даних.
2. Визначення кількості факторів.
3. Визначення факторного навантаження.
Навантаження - це фактично регресійний коефіцієнт, що показує, яку вагу має даний фактор для прогнозування значення відповідної змінної.
4. Інтерпретація факторів.
6.3. Центроідний метод Л. Терстоуна
Метод дозволяє виділяти декілька латентних і характерних факторів і дає можливість співвідносити факторне рішення з вихідними даними.
Основне співвідношення факторного аналізу:
 , j=1,2,3,...,n де
, j=1,2,3,...,n де
bi - факторні навантаження;
ej - залишковий фактор, незалежний від k загальних факторів;
zij - коефіцієнт факторного навантаження j-го фактора на i-ту змінну.
Загальна постановка задачі складається з:
- побудови та аналізу кореляційної матриці;
- визначення числа факторів;
- визначення факторного навантаження;
- інтерпретація факторів;
- визначення змістовного значення факторів.
Відповідно до постановки задачі факторному аналізу завжди передує кореляційний аналіз. В загальному випадку кореляційна матриця має вигляд:

де елементи головної діагоналі (rX1X1, rX2X2, ..., rXnXm) дорівнюють 1.
На основі цієї матриці будується редукційна матриця зі спільностями на головній діагоналі. Існують різні методи будування спільності, найпростіший з який є метод найбільшого елемента по рядку.Суть методу полягає в тому, що в рядку матриці R вибирається елемент із найбільшим абсолютним значенням і це найбільше значення записується на головній діагоналі:

Елементи, що знаходяться на перетині рядків і стовпців, називаються навантаженнями (loadings) змінних на фактори.
Далі визначається кількість факторів, обчислюються коефіцієнти факторного навантаження і надається змістовна інтерпретація факторам.
Для отримання навантаження першого фактора необхідно знайти суми стовпців редукційної матриці та суму кожного стовпця розділити на квадратний корінь суми всіх елементів цієї матриці:
 , де Т - сума всіх елементів матриці.
, де Т - сума всіх елементів матриці.
Для отримання навантаження другого фактора необхідно знайти залишкову матрицю, для цього від кожного елемента матриці віднімається добуток відповідних навантажень:
для елементів головної діагоналі - 
для інших елементів - 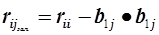
Далі необхідно знайти суми стовпців залишкової матриці (всі значення елементів матриці беруться по модулю) та суму кожного стовпця розділити на квадратний корінь із суми всіх елементів цієї матриці.
Якщо факторів більше ніж два, процедура повторюється знов.
Для відповідної інтерпретації даних треба відновити змінені знаки.
Для одержання значень факторних дисперсій застосовується формула:
 , де
, де
h1i- факторне навантаження на 1 фактор і змінної;
h2i- факторне навантаження на 2 фактор і змінної;
hij- факторне навантаження на j фактор і змінної.
При сумуванні квадратів факторного навантаження на фактор за всіма ознаками визначається оцінка внеску кожного фактора в сумарну дисперсію параметрів.
Питання для самоконтролю
1. Визначити основні етапи регресійного аналізу.
2. Охарактеризувати поняття залежної та незалежної змінної.
3. Визначити методи прогнозування залежної змінної за незалежними змінними.
4. Охарактеризувати основні цілі застосування регресійного аналізу.
5. Визначити роль коефіцієнта кореляції в регресійному аналізі.
6. Охарактеризувати регресійний коефіцієнт та вільний член регресійного рівняння.
7. Класифікувати фактори за різними ознаками.
8. Визначити поняття "факторна система".
9. Проаналізувати основні етапи факторного аналізу:
10. Проаналізувати алгоритм роботи центроідного методу в факторном аналізі.
Типовий приклад
Мета дослідження: Ознайомитись з основними складовими регресійного аналізу. Оволодіти навичками використання методу регресійного аналізу в дослідженнях систем міжнародних відносин/
Задача дослідження: провести змістовний аналіз досліджуваної системи за наступним планом:
1. Знайти лінійне регресійне рівняння для дискретної величини.
2. Знайти лінійне регресійне рівняння для неперервної величини.
Рішення задачі:
1. Дискретні величини:
За результатами проведеного аналітичного дослідження були отримані кількісні показники властивостей двох величин X таУ при 30 спостереженнях.Дані спостережень наведені в таблиці:
| Х | nj | ||||
| У | |||||
| ni |
На основі даних спостережень розраховується:
математичне очікування величини Х: Mx=6.83
математичне очікування величини У: My=3.00
середньоквадратичне відхилення величини Х: Sx=6.39
середньоквадратичне відхилення величини У: Sy=1.26
коефіцієнт кореляції між величинами Х та У: Rxy =-0.25
регресійний коефіцієнт:

вільний член:
b = My - a ·Mx =3.00-(-0.05·6.83)=3.33
Відповідно регресійне рівняння має вигляд:
y=-0.05x+3.33
2.Неперервні величини:
За результатами проведеного аналітичного дослідження були отримані кількісні показники властивостей двох величин X таУ за п’ять років (кількість спостереженьn=5). Потрібно побудувати регресійне рівняння.
Дані спостережень наведені в таблиці:
| № | Рік | Xi | Yi | Xi·Yi | Xi2 |
| 762,8 | 148,5 | 113275,8 | 581863,84 | ||
| 495,9 | 123,4 | 61194,06 | 245916,81 | ||
| 389,2 | 100,2 | 38997,84 | 151476,64 | ||
| 385,1 | 80,1 | 30846,51 | 148302,01 | ||
| 376,5 | 141752,25 | ||||
| СУМА | 2409,5 | 538,2 | 276693,21 | 1269311,55 |
За даними таблиці:
регресійний коефіцієнт дорівнює

вільний член дорівнює

Відповідно регресійне рівняння має вигляд: y=0.16x+30.42
математичне очікування величини Х: Mx=481,9
математичне очікування величини У: My=107,64
середньоквадратичне відхилення величини Х: Sx=147,09
середньоквадратичне відхилення величини У: Sy=25,3
коефіцієнт кореляції між величинами Х та У: Rxy =0,93
регресійний коефіцієнт:

вільний член:
b = My - a ·Mx =30.42
Відповідно регресійне рівняння має той самий вигляд:
y=0.16x+30.42
Індивідуальне завдання
Використовуючи основні процедури та методи системного аналізу продовжити самостійне дослідження системи, що була обрана для дослідження (індивідуальне завдання Тема №1) за наступним планом:
1. Використовуючи методи регресійного аналізу, знайти регресійні рівняння для досліджуваних дискретних та непевних величин (за схемою типового прикладу).
2. Побудувати графіки отриманих функцій.
Поради до виконання індивідуального завдання
Якщо за результатами кореляційного аналізу виявився сильний зв’язок між величина, дані цих величин можна використати для побудови лінії регресії. Якщо зв’язок був слабким, чи взагалі не спостерігався, знайдіть інші величини. Пам'ятайте, що регресійний аналіз завжди починається з кореляційного.
В висновку, аналізуючи побудований графік, спрогнозуйте майбутні стани системи.
Теми для обговорення
1. Приклади зростаючих та спадаючих процесів в системі міжнародних відносин.
2. Методи визначення числа факторів в системі.
3. Аналітичні обмеження на використання регресійного аналізу.
Зразок тестових завдань
1. Якщо регресійне рівняння має вигляд у= - 3х+5, це означає
a) чим більше Х тим більше У
b) чим менше Х тим більше У
c) чим менше Х тим менше У
2. Якщо редукційна матриця має вигляд:
0,8 0,5 0,8 0,2
0,5 0,5 0,3 0,4
0,8 0,3 0,8 0,5
0,2 0,4 0,5 0,5
скільки змінних досліджується:
a) 4
b) 8
c) 16
3. Якщо факторна система складається з 7 змінних, скільки основних факторів за правилом (k+n)<(n-k)2 формує цю систему:
a) 2
b) 3
c) 7
Основна література
1. Сізих Н.В. Теорія прийняття рішень в міжнародних відносинах: Навчальний посібник для лекційного курсу. - К.: Кобза, 2003. - 208 с.
2. Циба В.Т. Математичні основи соціальних досліджень: кваліметричний підхід. - К.:МАУП, 2002. - 248 с.
3. Международные отношения: социологические подходы / под ред. П.А. Цыганкова. – М., 2006. – 346 с.
4. Лигун А. А., Малышева А. Д. Математическая обработка результатов эксперимента. Днепродзержинск: ДИИ, 1992—47с.
5. Саати Т. Математические модели конфликтных ситуаций — М.: Сов. радио, 1989. — 304 с.
Дата добавления: 2014-12-30; просмотров: 535; Мы поможем в написании вашей работы!; Нарушение авторских прав |