
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
ТЕМА №3. випадковІСТЬ ТА ІМОВІРНІСТЬ
3.1. Базові поняття випадкової величини в системі
Для соціальних систем заповнювачами каналів зв'язку між елементами системи можуть бути:
- реальні (фізичні) предмети, з їх кількісним та якісним описом;
- інформація, у вигляді повідомлень про події в системі.
Існує тісний системний зв’язок між елементами системи та інформацією про них.
Величини, що можуть приймати різні значення в залежності від зовнішніх умов, називають випадковими чи стохастичними за природою.
Будь яка величина в системі є наслідком дії інших величин. Випадковою вона вважається тоді, коли зв’язок між причинами та наслідками не може бути встановлений відомими аналітичними методами. Це відбувається через недостачу знань, відсутності доступу до інформації та потрібного обладнання, чи небажання описувати процес повністю. Таким чином, випадковість фактично це міра недоступності знань для дослідника.
За типом випадкові величини поділяються на неперервні та дискретні.
Неперервні величини набувають будь які значення на заданому інтервалі.
Дискретні величини набувають конкретні, заздалегідь обумовлені значення.
Для випадкових величин використовують спеціальні статистичні методи їхнього опису та аналізу, що базуються на законах теорії ймовірностей.
3.2. Випадкова подія та її імовірність
Подія - будь який факт, який за результатом досліду може відбутися, чи не відбутися.
Елементарна подія –подія яку неможливо розкласти на менші події (множини).
Складна подія –подія яку можна розкласти на множину елементарних подій.
Події за результатом поділяються на:
- достовірні (відбудуться обов’язково);
- неможливі (не відбудуться ніколи);
- випадкові (можуть відбутися, чи не відбутися).
Імовірність – числова характеристика, що відображає можливість появи події за результатом експерименту, який повторюватися необмежену кількість разів.
Про імовірність події можна казати тільки в рамках певного дослідження.
Числове значення імовірності достовірної події дорівнює 1, неможливої дорівнює 0, випадкової знаходиться в інтервалі від 0 до1 (включаючи 0 та 1).
Якщо в конкретному експерименті поява події A виключає появу події В такі події називають несумісними.
Якщо в конкретному експерименті поява події A не виключає появу події В такі події називають сумісними.
Якщо в конкретному експерименті поява події `A, складається з того що подія A не відбувається такі події називають протилежними та їх імовірність пов’язана співвідношенням:
Р(`A) = 1 - Р(A)
Якщо в конкретному експерименті поява події A не залежить від появи події В такі події називають незалежними, в протилежному випадку - залежними.
Поняття залежність та сумісність подій характеризують різні властивості подій і їх не можна плутати. Несумісні події завжди залежні (згідно визначення несумісних подій, поява подіяA повністю виключає появу події В). Сумісні події можуть бути як залежними, тек і незалежними (згідно визначення сумісних подій, якщо подіяA відбулась то відбудетьсячи не відбудеться подіяВ залежить від умов експерименту).
Якщо імовірність того, що подія А відбудеться дорівнює P(А), то імовірність того, що подія не відбудеться, дорівнює: Р(`A) = 1 - Р(A)
Імовірність одночасного настання двох незалежних подій визначається добутком їхніх ймовірностей:
P(АВ) = P(А)•P(В).
Якщо результатом експерименту можуть бути несумісні у сукупності події А1, А2, ...Аn (за умовою, що тільки ці події можуть бути результатом), то їх множина утворює повну групу подій (вичерпну множину), для якої справедливе рівняння:
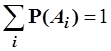
Якщо кожного разу, як відбувається подія А, відбувається подія В, то говорять, що подія В є наслідком події А, чи що з події А витікає подія В (позначається: А Ì ВчиВ É А ). Для таких подій справедлива нерівність:
Р(А) £ Р(В)
Умовна імовірність – імовірність здійснення події A при умові, що відбулась подія В (позначається як Р(A|В)).
Якщо події А та В незалежні, тоді Р(A|В)= Р(A).
Імовірність одночасного настання двох залежних подій визначається формулою Байеса
P(А|B)• P(B) = P(B|А)•P(А)
де ліворуч і праворуч записане те саме — імовірності одночасного настання двох залежних подій.
Якщо доповнити цю формулу загальним виразом безумовної імовірності події А, отримаємо формулу
P(А) = P(А|B)•P(B) + P(А|B)•P(B),
що означає: дана подія А може відбутися або після того як подія Bвідбулася, або після того, як воно не відбулася (B) — третього варіанту не істує.
Формули Байеса чи байесовский підхід до оцінки імовірнісних зв'язків для простих подій і дискретно розподілених випадкових величин відіграють вирішальну роль при прийняті рішення в умовах невизначеності. У цих умовах ключовою є стратегія керування, що базується на прогнозі апостеріорної імовірності події.
Якщо подія В є наслідком події А та утворює множину n подій: {B1,B2,...,Bn}, то імовірність події А розраховується за формулою:

яку називають формулою повної імовірності.
В цій схемі подія А відбувається тільки разом з якоюсьВi подією із множини {B1,B2,...,Bn}. Така Вi подія виступає як єдиноможлива подія з множини {B1,B2,...,Bn}, та взаємовиключаюча умова, що визначає появу події А, чи як гіпотеза, при підтверджені якої відбудеться подія А.
Ця формула прогнозує можливість появи події А за відомими апріорними ймовірностями здійснення гіпотези.
Апріорні та апостеріорні імовірності пов’язані співвідношенням, яке має назву теорема гіпотез чи формула Байеса:

яка оцінює здійснення кожної гіпотези, якщо подія А відбулась.
Якщо між подіями А і В немає зв’язку (одна не залежить від іншої), то дана формула перетворюється в тривіальну тотожність, ця обставина використовується при вирішенні задач оцінки тісноти зв'язків в кореляційному аналізі.
3.3. Імовірність як відносна частота появи події
Припустимо, що підсумком деякого дослідження може бути кінцеве число n несумісних та рівноможливих результатів і, що в m сприятливих результатах відбувається подія А. Тоді імовірність події А дорівнює співвідношенню числа сприятливих результатів mдо загального числа результатів n:
 , де W - відносна частота.
, де W - відносна частота.
Якщо порушується хоча б одна з трьох умов (кінцєвість, несумісність, рівновірогідність), ця формула не працює.
При використанні цього методу необхідно врахувати всі можливі сприятливі результати. Характерною помилкою для цього методу є поєднання різних (хоча і дуже схожих) сприятливих результатів в один.
Кількість всіх можливих сприятливих результатів легше підрахувати, якщо оформити результати дослідження у вигляді таблиці чи графа.
3.4. Дерево-граф результатів імовірності події
В ряді випадків дослідження може бути представлене як багатокроковий процес, в якому кожен попередній результат має декілька наступних результатів.
В загальному випадку результати кожного кроку дослідження не рівновірогідні. Подія, що цікавить дослідника, може відбутися після будь якого кроку.
При великій кількості результатів та кроків звичайний підрахунок імовірності події буде ускладнено. Такий процес можна спростити за допомогою звичайного дерева-графа результатів(Рис.3.1.)
Перший крок може мати два результати: (1:1) та (1:2) з відповідними ймовірностями Р1,1 та Р1,2. Кожен з цих результатів для другого кроку має роль початкового стану. На другому кроці подія (1:1) може мати результати (2:1), (2:2),(2:3) з відповідними ймовірностями Р2,1, Р2,2, Р2,3; а подія (1:2) результати (2:4), (2:5) з відповідними ймовірностями Р2,4, Р2,5 і т.д.

Рис.3.1. Дерево-граф результатів
Результати кожної події повинні створювати повну групу подій, що підтверджують умови:
Р1,1+Р1,2=1
Р2,1+Р2,2+Р2,3=1; Р2,4+Р2,5=1
Р3,1+Р3,2=1; Р3,3=1; Р3,4+Р3,5+Р3,6+Р3,7=1
Повна імовірність кожного результату визначається як добуток всіх ймовірностей, зазначених на відповідній гілці дерева, починаючи з даного результату і закінчуючи коренем дерева (початковим станом).
3.5. Розрахунок імовірності складної події, що представлена у вигляді комбінації елементарних подій
Складні події можуть бути представлені в вигляді комбінації елементарних подій. В найбільш розповсюджених задачах складну подію утворюють елементарні події, що відбуваються певну кількість разів, чи не менше (не більше) певної кількості разів. Для розрахунків імовірності складної події використовують формули суми та добутку подій, при відповідній послідовності:
1. Складна подія записується у вигляді комбінації елементарних подій, зв’язаних знаками суми та добутку.
2. Застосовуються формули імовірності суми та добутку подій.
3. Розраховуються імовірності елементарних подій (якщо вони не відомі).
4. Підраховується імовірність складної події, що досліджується.
3.6. Основні числові характеристики випадкових величин
Функцією розподілу випадкової величини Х називається функція F(x), що задає імовірність події, тобто імовірність того, що випадкова величина Х буде менша за деяке число х:
F(x)=P{X < x}
Функція розподілу має наступні властивості:
1. Функція F(x)зростаюча функція: F(x1) ³ F(x2) при x1 >x2
2. Функція F(x) неперервна зліва:
 (e>0)
(e>0)
3. Функція F(x) прагне до нуля, якщо х прагне до -¥

4. Функція F(x) прагне до одиниці, якщо х прагне до +¥
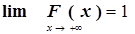
Математичне очікування випадкової величини (як дискретної так і неперервної) - це те, до чого прагне її середнє значення при досить великому числі спостережень.
Для дискретної випадкової величини: Mx = å Xi ·P(Xi);
де P(Xi) — імовірність того, що X прийме своє i-те чергове значення.
Для неперервної випадкової величини:
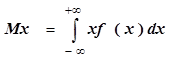
Медіана(серединне значення) випадкової величини називається таке значення випадкової величини X (позначається Me) при якому:
P(X<Me)=P(X>Me)=1/2
Для неперервної випадкової величини медіана знаходиться з умови:
F(Me)=1/2
Для дискретної випадкової величини медіана вираховується неоднозначно та практично не використовується.
Мода (найбільш імовірне значення) випадкової величини називається таке значення випадкової величини X (позначається Mо) для якого у випадках дискретного розподілу імовірність Р(Х=Мо), а випадках неперервного розподілу щільність імовірності F(Mo) має своє найбільше значення.
Дисперсієювипадкової величини називають очікування квадрата відхилення значення величини від її математичного очікування:
Для дискретної випадкової величини:

Для неперервної випадкової величини:

Розмірність дисперсії не збігається з розмірністю самої випадкової величини і це не дозволяє оцінити величину розсіювання. Тому найчастіше замість дисперсії використовується квадратний корінь з її значення — середньоквадратичне відхилення чи відхилення від середнього значення:

Значення Mx і SX іноді не несуть повної інформації. Тому часто для грубої оцінки "випадковості" величини використовують коефіцієнт варіації чи відношення кореня квадратного з дисперсії до величини математичного очікування:
Vx = SX/MX
3.7. Закони розподілу випадкових величин (параметрична статистика)
Закон розподілу випадкової величини - це ряд значень, які може приймати ця випадкова величини. Тобто набір всіх допустимих її значень.
Закон розподілу випадкової величини вважається заданим, якщо:
1. Визначена множина можливих значень випадкової величини.
2. З'ясовано засіб кількісного визначення імовірності попадання випадкової величини у довільній області цієї множини.
Встановити закон розподілу випадкової величини можна двома засобами:
1. За допомогою експерименту побудувати схему випадкових події.
2. За допомогою аналізу властивостей випадкової величини, визначити до якого з класичних законів розподілу відноситься ця величина.
Хоча існує нескінченна множина випадкових величин, законів розподілу набагато менше. Різні випадкові величини можуть мати однаковий закон розподілу. Такі розподіли називають теоретичними, а їх використання "параметричною статистикою". Для класичних законів розроблені методи розрахунку всіх показників розподілу, зафіксовані зв'язки між ними, побудовані алгоритми розрахунку і т.п.
3.8. Шкала для оцінки показників системи (непараметрична статистика)
Прийнято використовувати чотири види шкал:
Nom. номінальна шкала — застосовується до тих величин, що не мають природної одиниці виміру. Якщо деяка величина може набувати за номінальною шкалою значення X, Y чи Z, то справедливими вважаються тільки вирази типу:
(X¹Y), (X=Z).
Ord. порядкова (рангова) шкала — застосовується до тих величин, що не мають природних одиниць виміру, але дозволяють застосовувати поняття переваги одного значення над іншим. Іноді говорять про ранги значень таких величин. Якщо деяка величина може приймати на порядковій шкалі значення X, Y чи Z, то справедливими вважаються тільки вирази типу:
(X¹Y), (X=Z), (X<Y), (Y>Z), (Z£X), (Z³Y).
Дата добавления: 2014-12-30; просмотров: 356; Мы поможем в написании вашей работы!; Нарушение авторских прав |