
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
И закономерности их изменения
Понятие об электроотрицательности атомов впервые было применено еще в 1811г. шведским химиком И.Я.Берцеллиусом для классификации элементов, позднее (1858г.) это оно использовалось в работах С.Канницаро, И.Штарка. В 1916г. Дж.Н.Люис в в теории ковалентной связи рассматривал полярность как смещение центра тяжести валентного электронного облака в сторону "более электроотрицательного" атома. Однако количественная шкала электроотрицательностей впервые была разработана Л.Полингом в 1932 и последующих годах. В то же время, несмотря на столь долгую историю, до сих пор не выработано однозначного объективного критерия, характеризующего электроотрицательность атомов. Существует множество (более 20) систем или шкал, основанных как на экспериментальных результатах, так и на квантово-механических расчетах или их комбинации. Численные значения в разных системах в той или иной степени отличаются, но, во-первых, как правило, тенденции их изменения выглядят одинаково, а, во-вторых, сами абсолютные значения электроотрицательностей часто с помощью различных подгоночных преобразований нормируют по шкале Полинга. В рамках данного пособия будут кратко проанализированы лишь самые известные и чаще всего использующиеся.
Л.Полинг использовал понятие электроотрицательность как способность данного атома, конкурируя с другими атомами–партнерами, притягивать к себе общие валентные электроны химических связей. Таким образом, по Полингу: электроотрицательность – это свойство не изолированных, а связанных атомов (в отличие от энергии ионизации и сродства к электрону). Он использовал это понятие для объяснения того факта, что энергия гетероатомной связи А–В практически всегда больше среднеарифметического (или среднегеометрического) значения энергий гомоатомных связей А–А и В–В. Тогда при использовании среднеарифметической величины можно записать:
ЕА–В = 1/2·(ЕА–А + ЕВ–В) + ΔАВ.[17] (1.28)
Анализ большого числа экспериментальных фактов показал, что, если энергию связей выражать в кДж/моль, то ΔАВ можно связать с некоторыми с некоторыми константными характеристиками атомов (электроотрицательностями) выражением
ΔАВ = 96.12·(χА – χВ)2, (1.29)
из которого следует
| χА – χВ| = 0.102·  , (1.30)
, (1.30)
где χА , χВ – электроотрицательности элементов.
На основе этих выражений можно рассчитывать разность электроотрицательностей разных элементов. Для того, чтобы определить значение электроотрицательности для каждого элемента в отдельности необходимо какой-либо из них выбрать в качестве эталонного и постулировать для него значение χВ. В этом качестве Полинг выбрал водород, для которого вначале принял χН = 0, а позднее (в 1939г.) приписал водороду χН = 2.1, чтобы избежать отрицательных значений для электроотрицательности металлических элементов. Одновременно он изменил и формулу для расчета энергии ковалентной связи (1.28). Необходимость в этом возникла из-за того, что для гидридов щелочных металлов ΔМе–Н оказалась отрицательной величиной, что противоречит логике предложенного Полингом подхода. Для преодоления этой проблемы он изменил способ вычисления энергии ковалентной связи, заменив среднеарифметическое на среднегеометрическое усреднение:
ЕА–В = 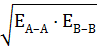 + ΔАВ. (1.31)
+ ΔАВ. (1.31)
Чтобы при этом сохранить ранее полученные значения электроотрицательностей элементов, оказалось необходимым заменить числовой сомножитель в выражении (1.30) на 0.089. Предложенные Полингом величины относительных электроотрицательностей широко применяются и в настоящее время. Вместе с тем, его работы стимулировали множество исследований, в которых уточнялась и расширялась экспериментальная база данных, предлагались новые критерии для построения систем электроотрицательностей (орбитальная, связевая, спектроскопическая, ионизационная и т.д.).
Исключительно ценно и широко используется химиками эмпирическое рассмотрение электроотрицательности как силы, действующей на электроны на расстоянии ковалентного радиуса
χЭ =  (1.32)
(1.32)
которое предложили Оллред и Рохов. Для нормировки к шкале Полинга используется выражение
χЭ = 0.359·  + 0.744. (1.33)
+ 0.744. (1.33)
Еще одна очень известная система, претерпевшая в дальнейшем разнообразные модернизации, была предложена Р.С.Малликеном. Его идея состояла в том, способность атомов конкурировать за общие электроны должны зависеть от их энергий ионизации и сродства к электрону. Например, тепловой эффект образования ионной молекулы А+В– должен зависеть от I1(А) и Еē(В):
ΔНА+В– = f [I1(А) – Еē(В)]. (1.34)
Тепловой эффект противоположного варианта перераспределения электрона:
ΔНА– В+ = f [I1(В) – Еē(А)]. (1.35)
Если реально молекула слабо поляризована с частичным смещением заряда в сторону атома В(атом В более электроотрицателен, χА < χВ), то
ΔНАδ+Вδ– = ΔНА+В– – ΔНА– В+= f [I1(А) – Еē(В)] – f [I1(В) – Еē(А)] (1.36)
или
ΔНАδ+Вδ– = f*[(I1(А) + Еē(А)) – (I1(В) + Еē(В))] =
= f**[I1(А) + Еē(А)] – f**[I1(В) + Еē(В)]. (1.37)
Такой способ перераспределения электрона оказался энергетически выгодным (ΔНАδ+Вδ– < 0), если
f**[I1(А) + Еē(А)] < f**[I1(В) + Еē(В)]. (1.38)
Логично эти функции считать электроотрицательностями атомов. В самом первом предложенном Малликеном варианте электроотрицательность была приравнена полусумме первой энергии ионизации и сродства к электрону:
χЭ (М) = ½·[I1(Э) + Еē(Э)] (1.39)
В дальнейшем было предложено несколько способов нормировать (сблизить) малликеновские электроотрицательности со шкалой Полинга. Лучшей оказалась формула, предложенная С.С.Бацановым с коллегами:
χЭ(Р) ≈ 0.4·[χЭ (М) – 0.4]. (1.40)
Таблица 1.9
Значения электроотрицательностей
для s– и р–элементов периодической системы
(1-я строка – χпо Полингу; 2-я и 3-я строки – χпо Малликену
(рассчитанная по формулам (1.39 ) и (1.40)); 4-я строка – χпо Оллреду-Рохову)
| H 2.10 7.18 (2.67) 2.20 | He – 12.18 (4.67) 5.50 | ||||||
| Li 0.98 2.58 (0.99) 0.97 | Be 1.57 4.56 (1.62) 1.47 | B 2.04 4.28 (1.51) 2.01 | C 2.55 6.00 (2.20) 2.50 | N 3.04 7.24 (2.70) 3.07 | O 3.44 7.54 (2.82) 3.50 | F 3.98 10.42 (3.97) 4.10 | Ne – 10.64 (4.06) 4.84 |
| Na 0.93 2.84 (0.94) 1.01 | Mg 1.31 3.72 (1.29) 1.23 | Al 1.61 3.22 (1.09) 1.47 | Si 1.90 4.76 (1.70) 1.74 | P 2.19 5.62 (2.05) 2.06 | S 2.58 6.22 (2.29) 2.44 | Cl 3.16 8.30 (3.12) 2.83 | Ar – 7.72 (2.89) 3.20 |
| K 0.82 2.42 (0.77) 0.91 | Ca 1.00 2.37 (0.75) 1.04 | Ga 1.81 3.19 (1.08) 1.82 | Ge 2.01 4.80 (1.72) 2.02 | As 2.18 5.31 (1.92) 2.20 | Se 2.55 5.89 (2.16) 2.48 | Br 2.96 7.61 (2.84) 2.74 | Kr – 6.79 (2.52) 2.94 |
| Rb 0.82 2.33 (0.73) 0.89 | Sr 0.95 2.09 (0.64) 0.99 | In 1.78 3.05 (1.02) 1.49 | Sn 1.96 4.27 (1.51) 1.72 | Sb 2.05 4.79 (1.72) 1.82 | Te 2.10 5.51 (2.00) 2.01 | J 2.66 6.73 (2.49) 2.21 | Xe – 5.85 (2.14) 2.4 |
| Cs 0.79 2.18 (0.67) 0.86 | Ba 0.89 2.37 (0.75) 0.97 | Tl 1.83 3.16 (1.06) 1.44 | Pb 2.06 3.89 (1.36) 1.55 | Bi 2.02 4.12 (1.45) 1.67 | Po 2.00 4.88 (1.75) 1.76 | At 2.20 6.00 (2.20) 1.90 | Rn – 5.16 (1.86) 2.06 |
Наиболее интересным в методе Малликена является возможность вычисления значений χЭ для разных валентных состояний, принимая в расчет энергии ионизации с тех орбиталей, которые задействованы в образовании конкретных связей (возможно в том или ином долевом участии). В этом случае легко показать, что χЭувеличивается в ряду sp3→sp2→sp-гибридизованных атомов. Например, электроотрицательность углерода в направлении кратных связей занижается до ~2.2 (при двойной) и ~ 2.1 (при тройной), а в противоположных, наоборот, растет (~3.1 и ~3.4, соответственно).
В настоящее время ионизационные модели, основанные на подходе, предложенном Малликеном, являются лучшими и наиболее корректными из теоретических методов определения электроотрицательности элементов. Они наиболее адекватно позволяют показать, что электроотрицательность атома может изменяться в зависимости от его окружения, степени окисления, валентного состояния (от процентного вклада тех или иных орбиталей в связывание).
Как видно из приведенных в табл. 1.9 данных, электроотрицательность элементов в периодах в целом растет, а в подгруппах (главных) в целом уменьшается. Обсуждать же детальные закономерности не имеет большого смысла, поскольку, как уже было сказано, электроотрицательность элементов, строго говоря, не является абсолютно неизменной величиной, а зависит от перечисленных выше параметров.
Проектное задание
Дайте объяснение причин принципиальной невозможности описать движение электронов в рамках классических представлений о траектории движения тела. Сформулируйте правила квантования и заселения атомных орбиталей электронами (определите границы применимости соответствующих положений). На основе современных представлений об электронном строении атомов объясните структуру периодической системы элементов. Сформулируйте закономерности изменения электронного строения атомов и ионов, причины и условия осуществления электронных проскоков. Учитывая влияние различных факторов, определяющих особенности притяжения электронов к ядру и межэлектронных взаимодействий, объясните закономерности изменения важнейших атомных свойств в периодах и подгруппах периодической системы элементов.
Вопросы для самоподготовки:
В рамках самоподготовки по данному модулю рекомендуется продумать следующие вопросы:
1. Почему даже с точки зрения классической механики в многоэлектронных атомах практически невероятны круговые стационарные орбиты?
2. Каково электронное строение лантаноидов и актиноидов? Как объяснить случаи электронных проскоков в соответствующих рядах?
3. Как будет меняться внешний вид графиков радиального распределения электронной плотности для l = 0, l = 1 при изменении направления радиус-вектора? Что такое узловые точки, узловые и граничные поверхности?
4. Как меняется вероятность электронных проскоков в рядах d–элементов, почему они гораздо чаще наблюдаются у элементов V-го периода?
5. Как объяснить характер изменения орбитальных и металлических радиусов в ряду 3d–элементов?
6. Сравните друг с другом первые, вторые, третьи и четвертые энергии ионизации Mg и Al? Объясните полученный результат.
7. Почему электроотрицательность элементов подгруппы ванадия в степени окисления +II растет, а в высшей – уменьшается? Как это должно отразиться на изменении характера связывания в соответствующих соединениях?
Дата добавления: 2014-11-13; просмотров: 394; Мы поможем в написании вашей работы!; Нарушение авторских прав |