Доверительный интервал для среднеквадратического отклонения .

Пусть неизвестны. Можно показать, что тогда случайная величина 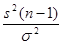имеет распределение с (n – 1) степенями свободы.По доверительной вероятности 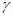определяют , по таблице квантилей распределения с n – 1 степенями свободы определяют квантили уровней и 1 - : , 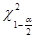. Имеет место соотношение

. Строим доверительный интервал для среднеквадратического отклонения

.

Объяснение причин, по которым параметры распределены по Стъюденту или , требуют более глубокого рассмотрения материала. Но для догадки можно использовать два известных результата:

- если x_{1, …}x_n распределены нормально, то имеет распределение с n степенями свободы

- если x распределена нормально, а y по с n степенями свободы, то случайная величина 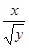распределена по Стъюденту.

Содержание