КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Интервальные оценки.
Доверительный интервал – это интервал  , такой, что
, такой, что 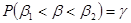 ,
,
где 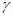 - доверительная вероятность.
- доверительная вероятность.
Общее правило построения доверительного интервала для любого параметра основано на центральной предельной теореме, по которой при больших n (n>50) оценка 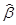 имеет нормальное распределение с
имеет нормальное распределение с 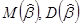 , если
, если 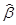 - несмещенная оценка, а функция распределения случайной величины
- несмещенная оценка, а функция распределения случайной величины 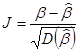 сходится по вероятности при
сходится по вероятности при 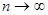 к функции стандартного нормального распределения.
к функции стандартного нормального распределения.
Квантиль 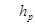 (уровня
(уровня 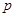 ) случайной величины X с функцией распределения F(x) – это такое значение
) случайной величины X с функцией распределения F(x) – это такое значение 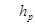 случайной величины X, что
случайной величины X, что 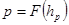 .
.
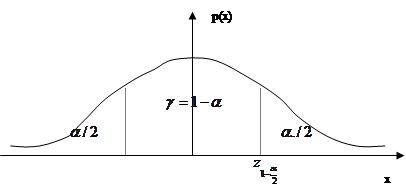
| Обозначим 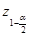 квантиль нормального распределения уровня квантиль нормального распределения уровня  , где , где  , , 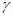 - доверительная вероятность, т.е. - доверительная вероятность, т.е.  , где , где 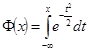 - функция - функция
|
стандартного нормального распределения. По симметрии плотности нормального распределения 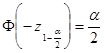 . Так как
. Так как  .
.
Так как распределение случайной величины 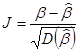 стремится к стандартному нормальному распределению, то
стремится к стандартному нормальному распределению, то 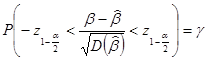 . Отсюда получаем доверительный интервал
. Отсюда получаем доверительный интервал
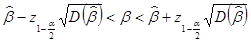 .
.
Дата добавления: 2014-12-30; просмотров: 301; Мы поможем в написании вашей работы!; Нарушение авторских прав |