КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Задача линейного прогноза.
|
Читайте также: |
Заданы характеристики 
случайного вектора 
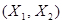. Вводится случайная величина – оценка 
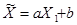- линейный прогноз. Вычислить 
, чтобы линейный прогноз был наилучшим среднеквадратическим (в смысле минимума погрешности оценки: 
).
.
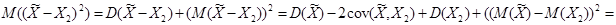
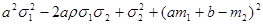За счет выбора 
можно лишь минимизировать последнее слагаемое, сделав его нулем: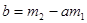 
.Теперь остается обеспечить минимум квадратного трехчлена от 
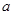(найти вершину параболы): 
. Подставляя это значение, найдем
. Вычислим погрешность оценки при этих значениях параметров
.
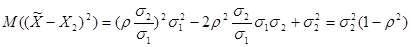При линейной зависимости 
оценка точна, погрешность равна нулю.
Чем меньше коэффициент корреляции, тем грубее оценка. В крайнем случае, при отсутствии корреляции (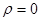 
) 
.
Лекция 7.
Законы больших чисел и центральная предельная теорема.
Дата добавления: 2014-12-30; просмотров: 22; Нарушение авторских прав
