
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Свойства ковариации.
1. 
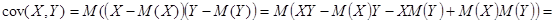
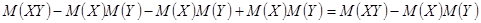
2. 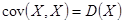
По свойству 1 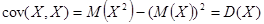
3.Если X, Y независимы, то 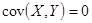 , (обратное неверно).
, (обратное неверно).
Если случайные величины независимы, то 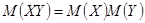 , тогда по свойству 1
, тогда по свойству 1 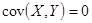 .
.
Случайные величины называются некоррелированными, если 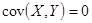 , из некоррелированности не следует независимость, из независимости следует некоррелированность.
, из некоррелированности не следует независимость, из независимости следует некоррелированность.
4. 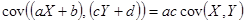
По свойству 1
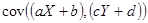 =
= 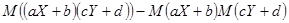 =
= 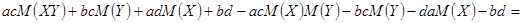 =
= 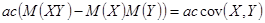
5. 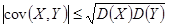
Рассмотрим случайную величину 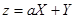 .
. 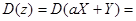
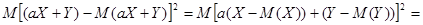
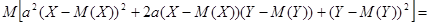
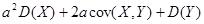 .
.
Заметим, что отсюда следует свойство дисперсии (при a =1)
 .
.
Так как 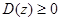 , то
, то 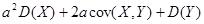
 . Это возможно только, если дискриминант этого квадратного трехчлена относительно a меньше или равен нулю. Выпишем это требование к дискриминанту:
. Это возможно только, если дискриминант этого квадратного трехчлена относительно a меньше или равен нулю. Выпишем это требование к дискриминанту:
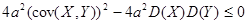 . Отсюда следует свойство 5.
. Отсюда следует свойство 5.
6.Для того, чтобы случайные величины были линейно зависимы (Y = aX +b), необходимо и достаточно, чтобы 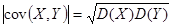
Необходимость. Пусть Y=aX+b. Тогда 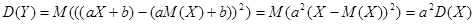

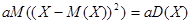 =
= 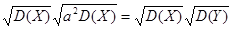
Достаточность. Пусть 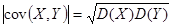 .Тогда (доказательство свойства 5)
.Тогда (доказательство свойства 5) 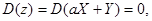 следовательно, z -
следовательно, z -  детерминированная величина, т.е.
детерминированная величина, т.е. 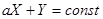 , поэтому величины X, Y – линейно зависимы.
, поэтому величины X, Y – линейно зависимы.
Коэффициентом корреляцииназывается 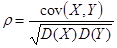 .
.
Дата добавления: 2014-12-30; просмотров: 700; Мы поможем в написании вашей работы!; Нарушение авторских прав |