Предельные теоремы.

Центральная предельная теорема – это любая теорема, ставящая условия, при которых функция распределения суммы индивидуально малых случайных величин с ростом числа слагаемых сходится к нормальной функции распределения.

Центральная предельная теорема подтверждает следующее: если исход случайного эксперимента определяется большим числом случайных факторов, влияние каждого из которых пренебрежимо мало, то такой эксперимент хорошо аппроксимируется нормальным распределением с параметрами 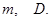, подобранными соответствующим образом.

Теорема Ляпунова.

Пусть X_k – независимые случайные величины, имеющие математические ожидания M(X_k) = m_k и дисперсии D(X_k) = D_k. Обозначим . Если можно подобрать такое , что , то при 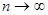равномерно по x.