
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Интегральная теорема Муавра – Лапласа.
Пусть производится n независимых испытаний, в каждом из которых с вероятностью p может появиться событие А. Обозначим  - число появлений события в k –ом испытании (
- число появлений события в k –ом испытании ( 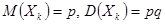 ). Обозначим
). Обозначим 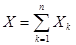 - общее число появлений события в n испытаниях (
- общее число появлений события в n испытаниях (  ). Обозначим
). Обозначим  . Тогда при
. Тогда при 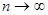
 равномерно по x.
равномерно по x.
Отсюда следует практическое правило вычисления

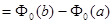 , где
, где 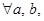
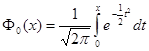 . Так как
. Так как 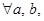 то заменим
то заменим 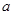 на
на 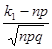 ,
,  на
на  ,
, 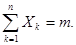 Получим формулу для вероятности нахождения числа успехов в заданном интервале:
Получим формулу для вероятности нахождения числа успехов в заданном интервале:
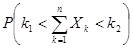 =
= 
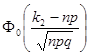 -
-  .
.
Заменим 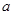 на
на 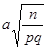 ,
,  на
на 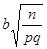 .
.
Тогда  .
.
Но 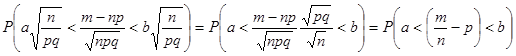 .
.
Поэтому справедлива формула для вычисления отклонения частоты от вероятности
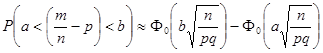 ,
,
Если интервал симметричный, т.е.  , то по нечетности функции Лапласа получим
, то по нечетности функции Лапласа получим
 .
.
Пример. Вероятность появления события p = 0,8. Сделано n = 100 независимых испытаний. Найти вероятность того, что событие произойдет не менее 75 и не более 90 раз.

Пример. Бюффон бросил монету 4040 раз и получил герб 2048 раз. Найти вероятность отклонения частоты появления герба от вероятности.
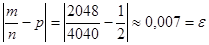

Дата добавления: 2014-12-30; просмотров: 318; Мы поможем в написании вашей работы!; Нарушение авторских прав |