Доверительный интервал для математического ожидания.

Если ГС имеет нормальное распределение, то и любая выборка распределена нормально. Известно, что сумма нормальных случайных величин тоже распределена нормально. Поэтому оценка математического ожидания – выборочное среднее – нормально распределенная случайная величина с - известно.

3) Поэтому, если 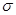известно,то , и доверительный интервал для математического ожидания строится так:

с доверительной вероятностью . Квантили проще всего искать по таблицам квантилей нормального распределения.

4) Если 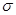неизвестно, то нормированная случайная величина (вместо 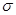подставлена его оценка s) уже не распределена нормально. Она имеет распределение Стъюдента с n-1 степенями свободы.Есть таблицы квантилей распределения Стъюдента. По доверительной вероятности 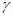определяют , по таблице квантилей определяют квантиль уровня . Затем по той же схеме строят доверительный интервал для математического ожидания .

Если n> 20, то квантиль можно искать по таблицам квантилей нормального распределения.