Краткие сведения о символическом методе

+7 (925) 393-3345;

+7 (499) 393-3345

Книги серии «Пробуждение сознания»

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

К КОНТРОЛЬНОЙ РАБОТЕ ДЛЯ СТУДЕНТОВ ЗАОЧНОГО ОБРАЗОВАНИЯ ПО ДИСЦИПЛИНЕ «ЭЛЕКТРОТЕХНИКА И ЭЛЕКТРОНИКА»

ГР………………

ФАКУЛЬТЕТ……………………………

Задача № 1. Рассчитать разветвлённую однофазную электрическую цепь переменного синусоидального тока символическим методом и построить в масштабе векторную диаграмму.

Задача № 2.Рассчитать трёхфазную электрическую цепь переменного синусоидального тока символическим методом с включением приёмников электрической энергии:

- по схеме звезда с нейтральным проводом и

- по схеме треугольником. Для обоих способов в масштабе построить векторные диаграммы.

Задача № 3.Исследование динамического режима работы биполярного транзистора типа КТ503Г включённого по схеме с общим эмиттером, представляющим самостоятельный однокаскадный усилитель переменного напряжения. Расчёт элементов схемы и исследование усилительных свойств однокаскадного усилителя на биполярном транзисторе.

Краткие сведения о символическом методе

Метод проводимости с графоаналитическими процедурами с использованием проекций при построении векторных диаграмм является наглядным, но неточным. Поэтому в настоящее время в электротехнике во всём мире широко используется более эффективный и весьма точный символический метод с использованием комплексных чисел.

Векторное представление токов, напряжений и эдс в цепях переменного тока базируется на сведениях тригонометрии и геометрии в объёме школьной математики старших классов. Проведённый, в прямоугольной системе координат Х и Y из начала координат вектор, с произвольным модулем, при его вращении с заданной постоянной угловой частотой 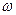от оси Х против часовой стрелки, даст за один оборот изменение своей проекции на ось Y по синусоидальному закону за время равное одному периоду Т. Приняв в качестве модуля вектора эдс, ток или напряжение, можно записать изменение проекций указанных величин на ось Y в виде их мгновенных изменений с той же угловой частотой

. (1)

Следовательно, мгновенные величины эдс, тока и напряжения, изменяющиеся по синусоидальному закону можно представлять векторами , как в действующих, так и в амплитудных значениях (при этом следует помнить связь между амплитудными и действующими значениями указанных величин с помощью ).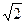

Математики ввели в декартовую систему координат новые обозначения осей: ось Y обозначили мнимой частью j , а ось Х вещественной частью «+» комплексного числа, которое может быть задано в любом квадранте комплексной плоскости с введёнными обозначениями (рис.1). Для произвольно взятого комплексного числа на комплексной плоскости, например в первом квадранте, можно после соединения этого числа с началом координат для введения вектора ОА (рис.2) представить комплексное число разными формами:

1. 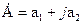– алгебраической;

2. – тригонометрической;

3. показательной.

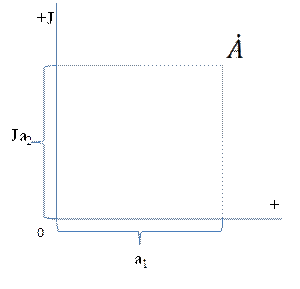
Рис. 1 Рис. 2

Алгебраическая форма записывается через сумму проекции а₁ комплекса на вещественную ось «+» и проекции jа₂ с учётом введённого обозначения для оси Y на мнимую ось «j» (см. рис. 1).

Тригонометрическая форма комплексного числа записывается через сумму проекций данного вектора на вещественную ось и мнимую ось с использованием свойств полученного прямоугольного треугольника. Проекция на вещественную ось, как прилежащий катет к углу прямоугольника, выражена произведением модуля вектора ОА и . Проекция же на мнимую ось выражена произведением модуля вектора ОА на , так как катет прямоугольника расположен против угла (см. рис. 2).

Поскольку конец вектора ОА совпадает с заданным комплексным числом и проекция вектора на мнимую ось представляет собой синусоидально изменяющуюся величину, которой можно представить изменение напряжений, токов и эдс переменного тока, поэтому наряду с векторным представлением указанные величины переменного тока могут быть представлены в комплексном виде. Из-за совпадения конца вектора с комплексным числом на комплексной плоскости представление напряжений, токов и эдс в комлексном виде для расчётов и анализа в цепях переменного тока получило название символического метода. Для угла тригонометрическая форма комплексного числа может быть записана как 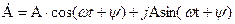, что означает наличие начального фазового сдвига относительно начала координат синусоидально изменяющихся переменных токов, напряжений, эдс во времени.

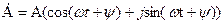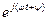Для представления векторов комплексными числами преобразуем тригонометрическую форму следующим образом. Вынесем в правой части тригонометрической формы модуль А за скобки и получим выражение . Математиком Эйлером доказано, что выражение равно величине , которая называется поворотным множителем. После чего появилась запись для показательной формы комплексного числа: .

Величину модуля в представленных формах комплексных чисел рассчитывают по формуле

А = , (2)

а угол – по формуле

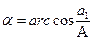. (3)

В отличие от механики вектора в электротехнике не имеют направления, так как они лишь вращаются с угловой частотой 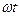в течение времени. После совершения любого количества целого числа оборотов вектора занимают своё исходное состояние с учётом начального фазового сдвига не равным нулю. Более того, на векторных диаграммах вектора занимают своё положение в зависимости от фазовых сдвигов относительно друг друга из-за наличия реактивных сопротивлений в цепях переменного тока. Поэтому при построении векторных диаграмм вектора не вращают, начальные фазовые сдвиги не наносят, а учитывают лишь относительные сдвиги между векторами, обозначаемые углом 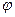(рис.3).

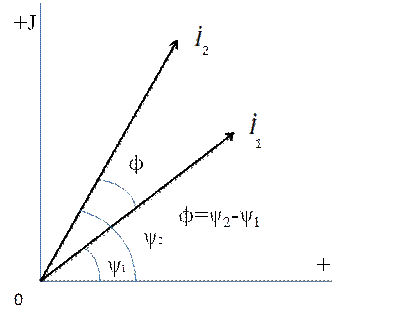
Рис. 3

Соответственно с учётом сказанного показательная форма комплексного числа записывается, как 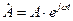. При угле = 0 вектор комплекса совпадает с вещественной осью, так как для t = 0 , а проекция вектора на мнимую ось равна нулю. В итоге комплексное число равняется, своему модулю 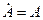и говорят, что комплекс 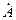задан вещественной частью A. Ток, напряжение и эдс в электротехнике, представленные комплексно, одновременно являются векторами.

При расчётах цепей переменного тока символическим методом очень важным является грамотное использование форм представления комплексного числа для реализации математических действий. С целью сокращения или недопущения ошибок при расчётах с комплексными числами электрических цепей переменного тока целесообразно операциисложения и вычитания производить в алгебраической форме. Операцииумножения, деления, возведения в степень, извлечения корнейвыполнятьв показательной форме. При операцияхделенияс мнимой частью в знаменателе необходимо знать существующие приёмы освобождения от мнимости в знаменателе. Необходимо помнить, что мнимость в квадрате требует изменения знака перед слагаемым в расчётах на противоположный знак.

При построениях векторных диаграмм для однофазных цепей переменного тока в комплексных осях, которые могут не обозначаться, для удобства построения векторной диаграммы по результатам расчёта однофазных цепей переменного тока за исходное базовое направление принимается, горизонтальная вещественная ось. Следует помнить, что вещественной оси всегда соответствуют активные составляющие векторов напряжений, токов и др. Мнимой оси – реактивные составляющие тех же векторов. Но на векторных диаграммах их не показывают, а наносят вектор под соответствующим углом к вещественной оси, при вращении векторов навстречу часовой стрелки углы откладываются положительные, а при вращении векторов совпадающим с направлением часовой стрелки углы откладываются отрицательные.

Примеры реализации основных математических действий

с использованием комплексных чисел

Полное сопротивление цепи переменного тока по закону Ома рассчитывается с использованием показательной формы, так как модуль сопротивления легко получают делением модулей напряжения и тока, а угол разностью углов числителя и знаменателя

Z = , Ом (4)

Из показательной формы сопротивления легко представить его в алгебраической форме, используя тригонометрическую форму представления комплекса

Z = , (5)

полученное выражение для сопротивления соответствует электрической цепи переменного тока, состоящей из активного сопротивления и индуктивности (RL – цепи).

Аналогично переходят к алгебраической форме сопротивления для RC – цепи

Z = , (6)

Из выражений (5) и (6) видно, индуктивное сопротивление соответствует положительному реактивному сопротивлению, а ёмкостное – отрицательному реактивному сопротивлению, что действительно соответствует теории цепей переменного тока.

Представим пример расчёта комплексной проводимости с наличием мнимости в знаменателе дроби

Y = 1/Z = . (7)

Выражение (7) соответствует комплексной проводимости для RL – цепи. Аналогично совершается переход к алгебраической форме комплексной проводимости для RC – цепи

Y = 1/Z = . (8)

В формулах (7) и (8) представлен приём освобождения от мнимости в знаменателе путём умножения числителя и знаменателя на сопряжённый комплекс знаменателя с дальнейшими алгебраическими преобразованиями (напомним, что j² = -1). Сопряженный комплекс означает противоположность исходному комплексу. Если исходный комплекс в расчётах имеет положительный знак в алгебраической форме, то в сопряжённом комплексе знак изменяется на противоположный. То же самое относится к показательной форме и тригонометрической.

Представим расчёт комплексной мощности. В данном случае мощность получают умножением комплекса напряжения 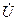на сопряжённый комплекс тока 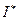. Например, известны исходные комплексы тока и напряжения: = 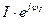и , тогда сопряжённый комплекс тока запишется как 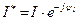, а комплексная мощность .

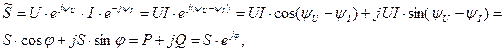(9)

где 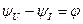– угол сдвига между векторами напряжения и тока;

UI = S – полная мощность.

P = 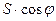– активная потребляемая мощность;

Q = – реактивная мощность.

Если цепь носит индуктивный характер, 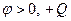(реактивная мощность положительна); если в этом случае сопротивление цепи имеет ёмкостной характер, (реактивная мощность отрицательна). Сказанное имеет большое значение при расчёте полной реактивной мощности для проверки баланса мощностей в электрических цепях (см. далее пример решения первой задачи контрольной работы).

Приведённые примеры показывают, что тригонометрическая форма комплексного числа служит для перевода алгебраической формы комплексов в показательную форму и наоборот. При этом модуль комплексного числа определяют по формуле (2), а угол 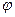по формуле (3).