
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Задания для контрольной работы.
Выбор номеров вопросов определяется последней цифрой.
Задание 1.Вычислить пределы:






Указания к заданию 1
Опр.Число А называется пределом функции f(x) при х, стремящемся к хо (или в точке хо),
если для любого  > 0 существует такое
> 0 существует такое  , что для всех х, удовлетворяющих
, что для всех х, удовлетворяющих
условиям |х – хо| <  , х¹х0, имеет место неравенство |f (x) – А| <
, х¹х0, имеет место неравенство |f (x) – А| <  .
.
Если А есть предел функции f (x) при х, стремящемся к хо, то пишут
 или
или  при
при  .
.
Если в определении предела вместо неравенств  , т.е.
, т.е. 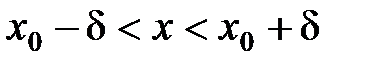 ,
,
х¹х0, рассмотреть неравенства  , то получим понятие правого предела. В
, то получим понятие правого предела. В
этом случае пишут 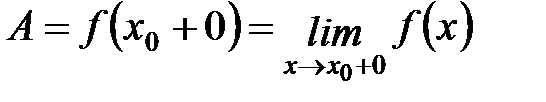
Рассматривая неравенства  , вводим понятие левого предела:
, вводим понятие левого предела:
 .
.
Предел (двусторонний) функции в точке хо существует в том и только в том случае, когда левый и правый пределы в этой точке существуют и совпадают: f (x0 –0)=f(x0 +0).
Опр. Число А называется пределом функции f (x) при x® +¥,  ,
,
если для любого  >0 существует такое М>0, что х > М Þ | f (x) – А | <
>0 существует такое М>0, что х > М Þ | f (x) – А | <  .
.
Опр. Число А называется пределом функции f (x) при x® -¥,  ,
,
если для любого  >0 существует такое М>0, что х < –М Þ | f(x) – А | <
>0 существует такое М>0, что х < –М Þ | f(x) – А | <  .
.
Опр. Число А называется пределом функции f (x) при x® ¥,  ,
,
если для любого  >0 существует такое М>0, что | х | > М Þ | f (x) – А | <
>0 существует такое М>0, что | х | > М Þ | f (x) – А | <  .
.
Замечание: вычисление любого предела начинается с подстановки предельного значения аргумента в функцию стоящую под знаком предела.
Пример 1. Вычислить предел 
Пример 2. Вычислить предел 
Пример 3. Вычислить предел 
Решение. Если подставить х = 1 в рассматриваемую функцию, получим 0 в числителе и знаменателе. Без дополнительных преобразований трудно сказать, к чему будет стремиться подобное выражение. Поэтому такие выражения называют неопределенностями, которые могут иметь вид:  Для каждой неопределенности существуют свои способы вычисления пределов.
Для каждой неопределенности существуют свои способы вычисления пределов.
Разложим числитель на множители: 


Замечание: а) замечательные пределы 

б) эквивалентности при  sin
sin  ,
,  ,
,  ,
,

 . При вычислении пределов можно пользоваться этими соотношениями.
. При вычислении пределов можно пользоваться этими соотношениями.
Пример 4. Вычислить предел 
Необходимо разделить числитель и знаменатель на переменную в наивысшей степени:




Задание 2. Производная и её приложения.
1. Найти производные функций: 
Найти интервалы выпуклости и точки перегиба графика функции: 
2. Найти производные функций: 
Найти наименьшее и наибольшее значения функции: 
3. Найти производные функций: 
Исследовать функцию на монотонность 
4. Найти производные функций: 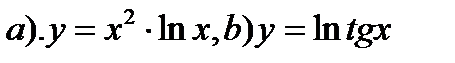
Исследовать функцию на экстремум 
5. Найти производные функций: 
Найти наименьшее и наибольшее значения функции 
6. Найти производные функций: 
Исследовать функцию на монотонность: 
7. Найти производные функций: 
Найти интервалы выпуклости и точки перегиба графика функции: 
8. Найти производные функций: 
Исследовать функцию на монотонность: 
9. Найти производные функций: 
Исследовать функцию на экстремум: 
10. Найти производные функций: 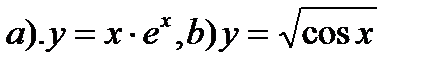
Найти наименьшее и наибольшее значения функции: 
Указания к заданию 2
Опр.Если при существует конечный предел дроби
существует конечный предел дроби  ,то этот предел называют производной функции
,то этот предел называют производной функции 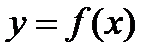 в точке х и обозначают символом
в точке х и обозначают символом  :
: 
Основные правила и формулы дифференцирования




Формулы: 

















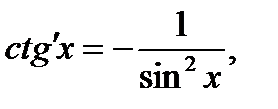












Дата добавления: 2015-01-01; просмотров: 315; Мы поможем в написании вашей работы!; Нарушение авторских прав |