
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Достаточные условия выпуклости (вогнутости) графика функции.
Если f’’(x)<0 в интервале (a, b), то график функции является выпуклым в этом интервале; если же f’’(x)> 0,то в интервале (a, b) график функции - вогнутый.
Точка (x0; f(x0)) графика функции, отделяющая его выпуклую часть от вогнутой, называется точкой перегиба.
Если x0 - абсцисса точки перегиба графика функции y=f(x0), то вторая производная равна нулю или не существует в этой точке. Точки, в которых f’’(x0)=0 или f’’(x0) не существует, называются критическими точками второго рода.
Если при переходи через критическую точку второго рода x0, вторая производная меняет знак, то точка (x0, f(x0)) есть точка перегиба.
Пример: Если продолжить рассматривать предыдущий пример, то найдём вторую производную: 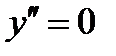 если
если 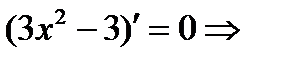
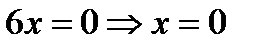 . Точек в которых функция не существует. - +
. Точек в которых функция не существует. - +
 0
0 

Так как вторая производная поменяла знак, то в точке х=0 имеется перегиб функции.
Задание 3.Найти интегралы:
3.1.  3.2.
3.2. 
3.3.  3.4.
3.4. 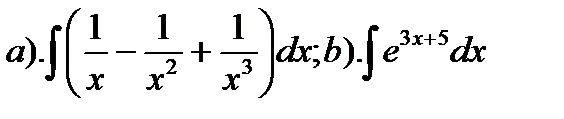
3.5.  3.6.
3.6. 
3.7.  3.8.
3.8. 
3.9.  3.10.
3.10. 
Указания к заданию 3.
Опр. Пусть функции f(x) и F(x) определены на интервале (a,b). Если функция F(x) имеет производную на (а,b) и для всех 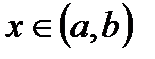 выполняется равенство
выполняется равенство  то функция F(x) называется первообразной для функции f(x) на интервале (a,b).
то функция F(x) называется первообразной для функции f(x) на интервале (a,b).
Пример: 

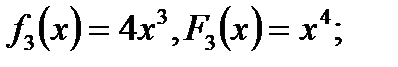
Если F(x) является первообразной для функции f(x) на интервале (a,b), то
очевидно, и функция F(x)+С где С-любая постоянная, является первообразной
для функции f(x), на интервале (a,b).Справедливо и обратное утверждение.
Опр. Совокупность всех первообразных функций для функции f(x) на интервале
(а,b), называется неопределенным интегралом от функции f(x) на этом интервале
и обозначается  Таким образом, если F(х) - какая-либо первообразная функции f(x) на интервале (а,b). то пишут
Таким образом, если F(х) - какая-либо первообразная функции f(x) на интервале (а,b). то пишут 
Операция нахождения неопределенного интеграла от данной функции называется интегрированием функции f(x).
Дата добавления: 2015-01-01; просмотров: 361; Мы поможем в написании вашей работы!; Нарушение авторских прав |