
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Линейные дифференциальные уравнения
Дифференциальное уравнение I порядка
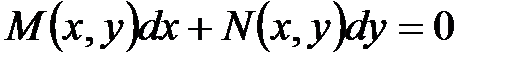 (1)
(1)
называется линейным, если отношение  содержит переменную y лишь в первой степени («линейно»). Линейное уравнение принято записывать в виде
содержит переменную y лишь в первой степени («линейно»). Линейное уравнение принято записывать в виде
 , (2)
, (2)
здесь  и
и  произвольные функции аргумента x. В частности, если
произвольные функции аргумента x. В частности, если 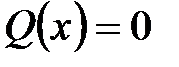 , то уравнение
, то уравнение
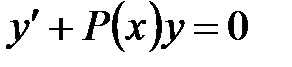 (3)
(3)
называется линейным однородным (или уравнением без правой части). Уравнение (3) легко решается разделением переменных, и общее решение имеет вид
 . (4)
. (4)
« Потерянное» при разделении переменных решение 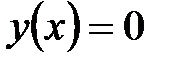 входит в полученную совокупность решений при С=0.
входит в полученную совокупность решений при С=0.
Если  , то уравнение (2) называется неоднородным линейным уравнением (или линейным уравнением с правой частью). Линейное уравнение решается методом вариации постоянных
, то уравнение (2) называется неоднородным линейным уравнением (или линейным уравнением с правой частью). Линейное уравнение решается методом вариации постоянных
Пример 1.Решить уравнение  .
.
Решение.Перепишем уравнение в виде 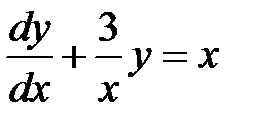 , это можно сделать, так как x=0не является его решением. Данное уравнение является линейным неоднородным уравнением.
, это можно сделать, так как x=0не является его решением. Данное уравнение является линейным неоднородным уравнением.
1). Выпишем линейное однородное уравнение, соответствующее исходному уравнению: 
 .
.
2). Разделим переменные в случае 
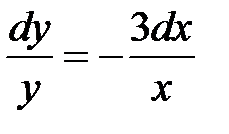 .
.
Решим последнее дифференциальное уравнение  ,
,  . В итоге получаем решение однородного линейного уравнения:
. В итоге получаем решение однородного линейного уравнения:  .
.
3). Выпишем вид общего решения  , где
, где  – неизвестная функция. Вычислим производную
– неизвестная функция. Вычислим производную  . Подставим
. Подставим  в исходное уравнение
в исходное уравнение  ,
, 
 .
.
В итоге получаем 
Иногда уравнение, не являющееся линейным относительно неизвестной функции  , становится линейным, если в нем поменять ролями переменные y и x, а именно взять за аргумент y, а за неизвестную функцию x, то есть
, становится линейным, если в нем поменять ролями переменные y и x, а именно взять за аргумент y, а за неизвестную функцию x, то есть  . Линейное уравнение такого типа можно записать в виде
. Линейное уравнение такого типа можно записать в виде  . (5)
. (5)
Пример 2. Решить уравнение  .
.
Решение.Данное уравнение не является линейным относительно неизвестной функции 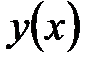 . Допустим, что неизвестной является функция
. Допустим, что неизвестной является функция  , уравнение можно переписать следующим образом:
, уравнение можно переписать следующим образом:
 ,
,  .
.
Полученное уравнение является линейным относительно функции  .
.
Решим линейное однородное уравнение  или
или 
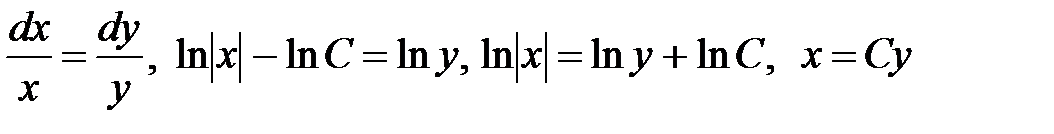 .
.
Выпишем вид общего решения линейного однородного уравнения  тогда
тогда 


 .
.
Интегрируя по частям, найдем  .
.

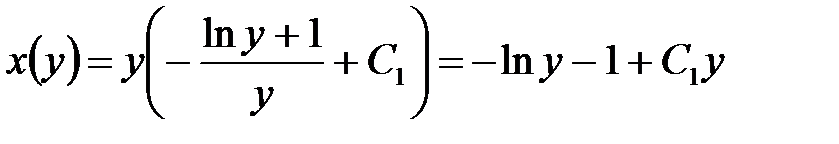 .
.
Дата добавления: 2015-01-01; просмотров: 272; Мы поможем в написании вашей работы!; Нарушение авторских прав |