Классическое определение вероятности

Классическое определение вероятности исходит из некоторой системы равновероятных событий.

Рассмотрим полную группу попарно несовместных равновозможных событий А₁, А₂, ... А_n. Добавим к этим n событиям невозможное событие V и сложные события, образованные с помощью операции сложения любого числа событий А₁, А₂, ... А_n с любыми номерами. Полученная система событий S исчерпывается конечным числом событий, если считать равносильные события просто тождественно равными друг другу.

Пусть полная группа попарно несовместных равновозможных событий состоит из двух событий А₁ и А₂. Тогда система S содержит следующие четыре события: V, A₁, A₂, A₁+A₂=U. Если же полная группа попарно несовместимых равновозможных событий состоит из трех событий A₁, A₂, A₃, то система S содержит восемь событий: V, A₁, A₂, A₃, A₁+A₂, A₁,+A₃, A₂+A₃, A₁+A₂+A₃=U.

Назовем для краткости событие A_i, (i=1,2, ... ,N) возможным случаем. Пусть событие B является некоторым событием системы S, тогда B представляется в виде суммы некоторых возможных случаев A_i. Слагаемые A_i , входящие в разложениеB, назовем случаями, благоприятствующими событиюB, а их число обозначим буквой m.

Вероятность Р(B) события B равняется отношению числа возможных случаев, благоприятствующих событию B, к числу всех возможных случав, то есть

(2.1)

Из определения вероятности следует, что для вычисления Р(B) требуется прежде всего выяснить, какие события в условиях данной задачи, являются возможными случаями, затем подсчитать число возможных случаев, благоприятствующих событию B и найти отношение числа благоприятствующих случаев к числу всех возможных случаев.

Пример 1. Известно, что среди 11 приборов имеется 3 непроверенных. Какова вероятность при случайном безвозвратном отборе 5 приборов обнаружить среди них 2 непроверенных.

Решение. Перенумеруем все 11 приборов. Возможными случаями будем считать комбинации по пять приборов из 11,отличающиеся только номерами приборов, входящими в каждую комбинацию. Отсюда следует, что число всех возможных случаев будет равно числу сочетаний из 11 элементов по 5 элементов:

.

Для подсчета возможных благоприятствующих случаев учитываем, что 2 из 3 непроверенных приборов можно извлечь способами. Кроме того, 3 проверенных прибора можно выбрать из 8 имеющихся проверенных различными способами. Каждый вариант из двух непроверенных приборов комбинируется с каждым вариантом из трех проверенных, следовательно, число возможных случаев m, благоприятствующих событию А, вероятность которого требуется найти, равно . Отсюда

Рассмотрим некоторые свойства вероятностей, вытекающие из классического определения.

1. Вероятность достоверного события равна единице. Достоверное событие U обязательно происходит при испытании, поэтому все возможные случаи являются для него благоприятствующими и

2. Вероятность невозможного события равна нулю. Число благоприятствующих случаев для невозможного события равно нулю (m=0), поэтому

3. Вероятность случайного события есть число, заключенное между нулем и единицей. В силу того, что дробь 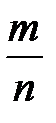не может быть числом отрицательным и большим единицы, справедливо неравенство: .