КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Интегрирование по частям.
Теорема.Если функции u(x) и v(x) дифференцируемы на интервале (а,b), то 
.
Таким образом, вычисление 
сводится к вычислению 
, которое может оказаться более простым.
Пример 1. Вычислить 
.
Положим u=x, 
, тогда 
Константу С при определении функции мы опускаем, так как она входит в окончательный ответ du=dx. Отсюда по формуле (2) имеем 
Метод интегрирования по частям применяют при вычислении следующих интегралов:
1) 
где Pn(x) – полином степени n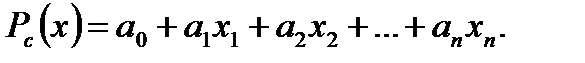 
В этих интегралах за u(x) принимается Pn(x) и интегрируют по частям n раз.
2 
В этих интегралах dv принимается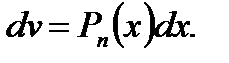 
Задание 4.Решить уравнение:
4.1. С разделяющимися переменными: 
4.2. Линейное первого порядка: 
4.3. Однородное первого порядка: 
4.4. Однородное первого порядка: 
4.5. С разделяющимися переменными: 
4.6. Линейное первого порядка: 
4.7. С разделяющимися переменными: 
4.8. Однородное первого порядка : 
4.9. Линейное первого порядка: 
4.10. С разделяющимися переменными: 
Указания к заданию 4
Дифференциальные уравнения являются одним из основных математических понятий, наиболее широко применяемых при решении практических задач. С помощью дифференциальных уравнений описывается динамика объектов или систем объектов.
Дифференциальным уравнением называется уравнение, содержащее производные неизвестной функции (или нескольких функций). Вместо производных в уравнение могут входить дифференциалы. Если неизвестные функции, входящие в дифференциальное уравнение, зависят только от одного аргумента, то дифференциальное уравнение называется обыкновенным дифференциальным уравнением.
Порядком дифференциального уравнения называется порядок старшей производной, входящей в уравнение.
Решением дифференциального уравнения n-ого порядка называется функция у(х), непрерывная на некотором интервале (а,b) вместе со своими производными до (n-1) порядка включительно и имеющая производную у(n)(x), такая что подстановка функции у(х) в исходное дифференциальное уравнение обращает его в тождество.
Заметим, что процедура решения простейшего дифференциального уравнения 
означает нахождение функции по ее производной, то есть, сводится к нахождению неопределённого интеграла 
. Произвольная константа С означает, что дифференциальные уравнения имеют бесконечные множества решений.
Дата добавления: 2015-01-01; просмотров: 98; Мы поможем в написании вашей работы!; Нарушение авторских прав |