Элементы комбинаторики.

Комбинаторика – это один из разделов дискретной математики, который приобрел большое значение в связи с использованием его в теории вероятностей, математической логике, теории чисел, вычислительной математике.

Человеку часто приходится иметь дело с задачами, в которых надо подсчитать число всех возможных способов расположения некоторых предметов, или число возможных способов осуществления некоторого действия. Такие задачи называются комбинаторными.

Комбинация – это соединение чего-либо в определенном порядке. К простейшим комбинациям относятся перестановки, размещения и сочетания. Перестановки – это комбинации, состоящие из одних и тех же п элементов и отличающиеся порядком этих элементов. Число всех возможных перестановок из n элементов вычисляется по формуле

Р_n=п!(1)

Заметим, что по определению п!= 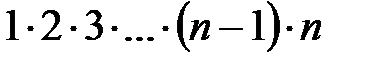и 0!= 1, 1!= 1 .

Пример 1.Определить число флагов с четырьмя горизонтальными поло­сами из красного, белого, синего и желтого цвета.

Решение.В нашем случае число элементов n = 4, поэтому Р₄ = 4!= = = 24 варианта.

Размещения – это комбинации, составленные из п различных элементов по т штук и отличающиеся друг от друга либо составом элементов, либо их порядком. Число всех возможных размещений из п элементов по т штук вычисляется по формуле

. (2)

Пример2. Определить число двухцветных флагов с горизонтальными полосами из красного, белого, синего и желтого цвета.

Решение.В нашем случае число элементов п = 4, т = 2, поэтому

=12 вариантов.

Сочетания – это комбинации, составленные из п различных элементов по т штук, которые отличающиеся хотя бы одним элементом. Порядок элементов не важен. Число всех возможных сочетаний из п элементов по т штук вычисляется по формуле

.(3)

Пример3. В бригаде 12 человек: 5 женщин и 7 мужчин. Сколько различных вариантов команд из трех человек можно составить? Сколько вариантов женских команд? Сколько вариантов мужских команд?