Теоремы сложения и умножения вероятностей

Если известны вероятности данных событий А₁, А₂, ... А_n, то на основе теорем сложения и умножения вероятностей можно найти вероятность любого события, полученного из данных с применением операций сложения, умножения событий и противоположного события.

Прежде чем рассматривать теоремы сложения и умножения, определим основные понятия.

Несколько событий называются несовместнымив данном опыте, если никакие два из них не могут появиться вместе в результате испытания. Если события могут появляться одновременно в данном опыте, то они называются совместными.

Например, при бросании одной монеты события А= "Выпадение орла" и В= "Выпадение решки" вместе произойти не могут, поэтому они несовместны. Если изменить условия опыта и бросить две монеты, то события АиВ будут совместными.

Два события называются независимыми,если появление одного из них не меняет вероятности наступления другого. В противном случае события называются зависимыми,а вероятность каждого из них, найденная при условии, что другое событие произошло, называется условной вероятностьюи обозначается Р(А/В), Р(В/А).

Например, в урне находится 3 синих и 4 зеленых шара. Событие А заключается в том, что из урны вынули синий шар, событие В состоит в том, что из урны вынули зеленый шар. Если вынутый синий шар не был возвращен назад в урну до того, как был вынут зеленый шар, то события А и В будут зависимыми, так как вероятность события В, вычисленная по формуле классической вероятности, в данном случае будет равна 4/6, и эта вероятность отлична от вероятности события 4/7, то есть события зависимы.

Если же вынутый синий шар был возвращен назад, а затем вынут зеленый, то Р(В/ А) = Р(В). И в этом случае события будут независимыми.

Теоремы сложения и умножения вероятностей.

Теорема 1.Вероятность противоположного события получается в результате вычитания из 1 вероятности события А, то есть .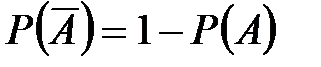

Теорема 2. Вероятность произведения двух независимых событий равна произведению вероятностей этих событий:

Пример 1.Студенты Симонов и Миронов хорошо занимались по математике в течение года. Однако перед экзаменом студенту, как всегда, не хватает одного дня. Симонов и Миронов пришли на экзамен, подготовив каждый 22 теоретических вопроса и 24 практических из 25-ти. Преподаватель решил поощрить студентов за хорошую учебу и предложил Симонову ответить на теоретический вопрос, а Миронову – решить задачу. Какова вероятность того, что Симонов сдаст экзамен, а Миронов не сдаст?

Решение.Введем в рассмотрение события: А - Симонов сдал экзамен; В - Миронов сдал экзамен. По классической формуле вероятности находим P(A)= , Р(В) = . Отсюда вероятность события 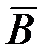, заключающегося в том, что Миронов не сдал экзамен, равна

События A и 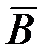независимы, поэтому

Теорема 3. Вероятность произведения двух зависимых событий равна произведению вероятности одного из них на условную вероятность другого, найденную в предположении, что первое событие произошло, то есть. .

Пример 2Из группы туристов в 36 человек, среди которых одинаковое число мужчин и женщин, случайным образом выбирают двоих. Какова вероятность того, что оба выбранных человека будут мужчинами?

Решение.Рассмотрим события: А – первый выбранный человек мужчина; В – второй выбранный человек мужчина. По формуле классической вероятности Р(А)= . В данной задаче событие В зависит от А и . Отсюда .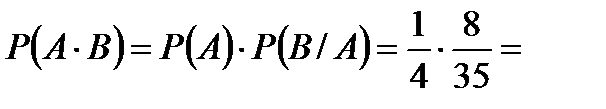

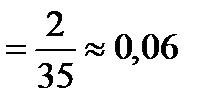Теорема 4.Вероятность суммы двух несовместных событий равна сумме вероятностей этих событий, то есть .

Пример 3. В агентстве на 15 число в наличии 7 путевок в Тунис, 3 – в Испанию и 2 – в Италию. Клиент берет одну путевку. Какова вероятность того, что это будет путевка в Европу?

Решение.Введем в рассмотрение события: А – клиент выбрал путевку в Тунис;

В – клиент выбрал путевку в Испанию; С – клиент выбрал путевку в Италию.

Событие В+С означает, что выбрана путевка в Испанию или Италию вынут. Поскольку события В и С несовместны, то Р(В + С) = Р(В) + Р(С) .

По формуле классической вероятности . Следовательно, .

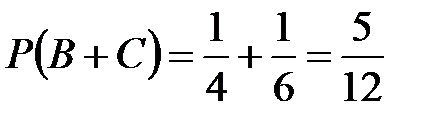Теорема5. Вероятность суммы двух совместных событий равна сумме вероятностей этих событий без вероятности их произведения: .

Пример 4.В урне находится 10 шаров, занумерованных числами от 11 до 20. Из урны наугад извлекают шар. Найти вероятность того, что номер извлеченного шара окажется кратным 2 или 3.

Решение.Введем в рассмотрение события: А – номер извлеченного шара кратен 2 (числа 12, 14, 16, 18, 20). Общее число благоприятных исходов равно 5, тогда . В – номер шара кратен 3 (числа 12, 15, 18) и . События А и В совместны (номера 12 и 18 подходят для обоих событий), поэтому .