Достаточные признаки существования экстремума

Правило 1. Если при переходе (слева направо) через стационарную точку x₀, производная f’(x₀) меняет знак с плюса на минус, то в точке x₀ функция f’(x₀) имеет максимум; если с минуса на плюс, то минимум; если знак не меняет, то экстремума нет.

Правило 2. Пусть функция f(x) дважды дифференцируема и имеет непрерывную вторую производную в точке x₀ и в некоторой ее окрестности, тогда если f’(x₀)=0, a f’’(x₀), то в точке х₀ функция f(x₀) достигает экстремума:

1) максимума, если f’’(x₀)<0. 2) минимума, если f’’(x₀)>0.

Пример: Используя ранее рассмотренный пример, можно увидеть, что производная при переходе через точки -1 и 1 меняет знак, следовательно, в этих точках имеется экстремум, причем в точке -1 - максимум, а в точке 1 - минимум.

-1 1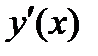

в). Выпуклость. Вогнутость. Точки перегиба.

График функции y=f(x) называется выпуклым в интервале (а, b), если он расположен ниже касательной. проведенной в любой точке этого интервала (рис. З).

График функции y=f(x) называется вогнутым на интервале (а, b), если он расположен выше касательной, проведенной в любой точке этого интервала (рис. 4).