
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Однородные дифференциальные уравнения.
Если в уравнении 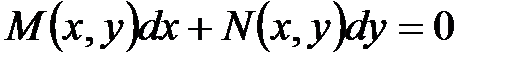 (1)
(1)
функции М(x,y) и N(x,y) являются однородными функциями одной и той же степени, то уравнение (1) называется однородным.
Приведенное свойство однородных функций нулевого порядка используется при решении однородных дифференциальных уравнений, то есть имеет место равенство ƒ(x,y)=  . Замечая, что в правой части стоит функция только одного аргумента
. Замечая, что в правой части стоит функция только одного аргумента  , и обозначая её через
, и обозначая её через  , мы видим, что однородное уравнение всегда можно представить в виде
, мы видим, что однородное уравнение всегда можно представить в виде  (2)
(2)
При произвольно заданной непрерывной функции j переменные не разделяются. Но так как в правую часть переменные входят только в комбинации  , то можно ожидать, что уравнение упростится, если ввести подстановку
, то можно ожидать, что уравнение упростится, если ввести подстановку 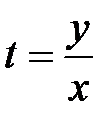 , откуда
, откуда
y=tx, (3) тогда  t+x
t+x  . (4)
. (4)
Подставим выражения (3) и (4) в уравнение (2)  , или
, или  .
.
Таким образом, мы получили уравнение с разделяющимися переменным  (5)
(5)
В случае, когда  (то есть
(то есть  ) уравнение (2) имеет вид
) уравнение (2) имеет вид 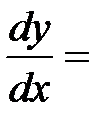
 , которое интегрируется с разделением переменных. Его общее решение
, которое интегрируется с разделением переменных. Его общее решение  .
.
Алгоритм решения однородного дифференциального уравнения:
1. Ввести новую функцию t =  и подставить y = t
и подставить y = t  x и
x и  t+x
t+x  в уравнение (2).
в уравнение (2).
2. В новых переменных t и x получить уравнение с разделяющимися переменными и найти его общее решение.
3. В полученном решении произвести обратную замену переменных t =  и выписать решение исходного однородного уравнения.
и выписать решение исходного однородного уравнения.
Пример 2.Решить уравнение  .
.
Решение.Разделим числитель и знаменатель правой части на x2:  . Введем замену
. Введем замену  , тогда наше уравнение перепишется следующим образом. После упрощения получаем
, тогда наше уравнение перепишется следующим образом. После упрощения получаем  . Проинтегрируем последнее уравнение
. Проинтегрируем последнее уравнение  . Разложим подынтегральное выражение на элементарные дроби
. Разложим подынтегральное выражение на элементарные дроби  .
.
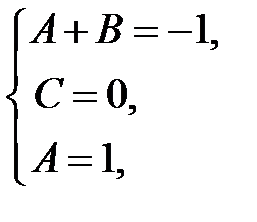 Þ
Þ  получаем в итоге
получаем в итоге  .
.
Вычислим интеграл 
Окончательно получаем  , или
, или  .
.
Делая обратную замену, получаем  или
или 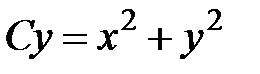 .
.
Дата добавления: 2015-01-01; просмотров: 253; Мы поможем в написании вашей работы!; Нарушение авторских прав |