IV)23)Достатня ознака збіжності для знакододатних рядів.

(Ознака порівняння рядів; ознака Даламбера; радикальна ознака Коші; інтегральна ознака Коші)

Означення: знакододатний ряд – ряд вигляду U₁+U₂+…+U_n+…, всі члени якого є додатними.

1) Ознака порівняння рядів.

Складаємо геометричний прогресію або гармонійний ряд і порівнюємо. Якщо порівняємо з розбіжним рядом, всі члени якого менше відповідних членів шуканого ряду, то шуканий ряд – теж розбіжний, якщо більшіші, то шуканий ряд – збіжний. Якщо порівнюємо із збіжним рядом, всі члени якого більше відповідних членів шуканого ряду, то шуканий ряд – теж збіжний, якщо менші, то шуканий ряд є розбіжним.

Гармонійний ряд – ряд вигляду:

Приклад:

Порівнюємо з гармонійним рядом, який є розбіжний.

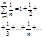
маємо:

ÞРяд розбіжний.

2) Ознака Даламбера:

Якщо для знакододатного ряду

існує

то, якщо:

а)D>1, ряд – розбіжний

б)D<1, ряд – збіжний

в)D=1, –???

3) Радикальна ознака Коші.

а)k<1, ряд – збіжний

б)k>1, ряд – розбіжний

в)k=1, – ???

4) Інтегральна ознака Коші.

Беремо ò від Un-члена ряду. Якщо невласний інтеграл збіжний, то ряд – збіжний, якщо ж розбіжний, то ряд – розбіжний.