IV)24) Знакопочергові ряди. Ознака Лейбніца.

Означення: Знакопочерговий ряд – ряд вигляду:

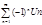
Для дослідження знакопочергового ряду на абсолютну і умовну збіжність складається ряд з абсолютних величин.

Означення: Знакозмінний ряд називається абсолютно збіжним, якщо збігається ряд із абсолютних величин членів знакозмінного ряду.

Означення: Знакозмінний ряд називається умовно збіжним, якщо цей ряд збігається, а ряд із абсолютних величин його членів розбігається.

Ознака Лейбніца.

Теорема: Якщо члени знакопочергового ряду спадають по абсолютній величині і границя абсолютної величини загального члена ряду = 0, то ряд збігається. Коротко цю теорему можна записати так:

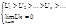
Наслідок1:

Знак суми збіжного знакопочергового ряду такий же, як і знак першого члену ряду.

Наслідок2:

Якщо знакопочерговий ряд збігається, то його сума за абсолютною величиною не перевищує перший член ряду, тобто |S|<|U₁|.

Наслідок3:

Якщо при обчисленні суми збіжного знакопочергового ряду обмежитись тільки першими n членами, а всі інші відкинути, то похибка за абсолютною величиною не перевищить першого із відкинутих членів.

Наслідок4:

Якщо для ряду не виконується умова теореми Лейбніца:

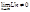
то ряд є розбіжним, оскільки не виконується необхідна умова збіжності.

(IV)25) Функціональні ряди.Область збіжності ряду. Степеневі ряди. Теорема Абеля. Інтервал і радіус збіжності степеневого ряду.

Означення: Ряд вигляду U₁(x)+U₂(x)+…+U_n(x)+…, де членами рядуU_n(x) є ф-ції від аргументу х, називається функціональним рядом. При х=х₀ функціональний ряд перетворюється на на числовий ряд.

Означення: Всі значення аргументу х, при яких функціональний ряд збігається, називаються областю збіжності функціонального ряду.

Степеневі ряди:

Означення: Функціональний ряд вигляду a₀+a₁x+a₂x²+…+a_nxⁿ+… називається степеневим рядом, його загальний член U_n(x)=a_nxⁿ, а числа а₀,а₁,а_2,...,а_n,... – називають коефіцієнтами степеневого ряду. Степеневий ряд можна записати як:

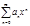
Степеневий ряд може мати вигляд: a₀+a₁₍x-с)+a₂₍x-с)²+…+a_n(x-с)ⁿ+… Такий ряд за допомогою заміни х-с=у зводиться до звичайного степеневого ряду.

Теорема Абеля.

Якщо степеневий ряд:

1) якщо при х=х₀, то він абсолютно збігається для будь-якого х, що задовольняє нерівність |x|<|x₀|;

2) якщо ряд розбігається при х=х₁, то він розбігається при всіх х, що задовольняють нерівніст |x|>|x₁|.

Інтервал і радіус збіжності степеневого ряду.

Як наслідок із теореми Абеля для Степ. Р. існує інтервал збіжності з центром в точці х₀.

Означення: Інтервалом збіжності Степ. Ряду називається такий інтервал, у всіх внутрішніх точках якого ряд збігається абсолютно, а для всіх точок |x|>R ряд є розбіжним, при цьому число R>0 називається радіусом збіжності ряду.

Зауваження:

На кінцях інтервалу збіжності, тобто в точках x=-R, x=R ряд може як збігатись, так і розбігатись. Це питання потребує спеціального дослілження в кожному випадку.