Уравнение поверхности в пространстве. Плоскость

Введем в пространстве прямоугольную декартову систему координат. Положение любой точки М пространства определяется ее координатами х, у, z.

Поверхность в пространстве рассматривается как множество точек, координаты которых удовлетворяют некоторому уравнению с тремя переменными F(x, y, z)=0. Этому уравнению не могут удовлетворять координаты никакой точки, не лежащей на поверхности. В этом случае уравнение F(x, y, z)=0 называют уравнением поверхности.

Пример № 7

Рассмотрим сферу радиуса R с центром в точке М₀(х₀, у₀, z₀). Так как любая точка М(х, у, z) сферы отстоит от центра на расстояние, равное радиусу сферы, то

или .

Получим уравнение

,

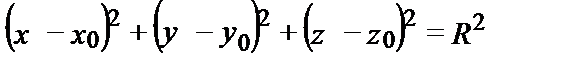которое и является уравнением сферы.

Простейшей поверхностью является плоскость. Получим уравнение плоскости, проходящей через данную точку перпендикулярно данному вектору.

Пусть даны точка М₀(х₀, у₀, z₀) и вектор , перпендикулярный плоскости.

Если точка М(х, у, z) – любая точка плоскости, то вектор лежит в плоскости и должен быть перпендикулярен вектору , т. е. скалярное произведение этих векторов равно нулю:

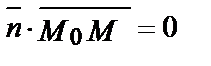
Запишем это условие в координатах.

;

Условие перпендикулярности примет вид:

А × (х–х₀) + В × (у–у₀) + С × (z–z₀) = 0 (7)

Полученное уравнение и является уравнением плоскости, проходящей через точку М₀(х₀, у₀, z₀) перпендикулярно вектору , который называют нормальным вектором плоскости.

Это уравнение легко привести к виду:

А × х + В × у + С × z + D = 0 (8)

– общее уравнение плоскости.

Заметим, что уравнение плоскости является уравнением первой степени с тремя переменными. Поэтому плоскость называют поверхностью первого порядка. Ранее полученное уравнение сферы – второй степени относительно х, у, z. Поэтому сфера – поверхность второго порядка.

Рассмотрим уравнения некоторых плоскостей.

Если плоскость проходит через начало координат, то свободный член D в общем уравнении (8) плоскости равен нулю, и уравнение плоскости имеет вид:

А × х + В × у + С × z = 0.

Уравнение координатной плоскости Оху можно получить, если в качестве нормального вектора взять вектор , где точка М₁(0,0,1), точка О(0,0,0). Тогда и уравнение координатной плоскости Оху: z=0. Аналогично,

х=0 – уравнение плоскости Оуz,

у=0 – уравнение плоскости Охz.

Очевидно, что уравнения х=a, у=b, z=c определяют три плоскости, параллельные трем координатным плоскостям.

Угол между плоскостями, заданными своими общими уравнениями:

А₁ × х + В₁ × у + С₁ × z + D₁ = 0 и

А₂ × х + В₂ × у + С₂ × z + D = 0

равен углу, образованному нормальными векторами и и вычисляется по формуле

.

Условие перпендикулярности двух плоскостей:

А₁ × А₂ + В₁ × В₂ + С₁ × С₂ = 0.

Условие параллельности:

.

Например, плоскости

2х + 3у – 5z + 7 = 0 и 4х + 6у – 10z – 1 = 0 – параллельны.

Прямую в пространстве можно рассматривать как линию пересечения двух плоскостей А₁ × х + В₁ × у + С₁ × z + D₁ = 0 и А₂ × х + В₂ × у + С₂ × z + D₂ = 0.

Поэтому прямая в пространстве определяется системой двух уравнений первой степени с тремя переменными х, у, z:

общие уравнения прямой. (9)