Обзор кривых второго порядка

Прямая на плоскости является линией первого порядка, так как определяется уравнением первой степени с двумя переменными. Рассмотрим кривые второго порядка, то есть линии, определяемые в декартовых координатах уравнениями второй степени. Установлено, что таких линий всего четыре: окружность, эллипс, гипербола и парабола.

В п. 4 было получено уравнение окружности с центром С(х₀, у₀) и радиусом r:

(х–х₀)² + (у–у₀)² = r² (14)

Из этого уравнения можно получить так называемое общее уравнение окружности: x²+y²+m×x+n×y+p=0. Заметим, что коэффициенты при х² и у² в уравнении окружности одинаковы. Если же в уравнении коэффициенты при х² и у² будут разными по величине, но одного знака, то такое уравнение будет определять эллипс.

Простейшее (каноническое) уравнение эллипса имеет вид:

(15)

Чтобы построить такой эллипс, отметим точки пересечения эллипса с осями координат: А₁(a, 0), А₂(-а, 0), В₁(0, b), В₂(0, -b), называемые вершинами эллипса. Расстояние между вершинами |А₁А₂|=2а и |В₁В₂|=2b называют осями, а числа а и b – полуосями эллипса (а>0, b>0). Из уравнения (15) эллипса видно, что эллипс – фигура, симметричная относительно обеих осей и начала координат. Для точного построения эллипса используем определение:

Эллипсом называется множество точек плоскости, сумма расстояний от каждой из которых до двух данных точек F₁ и F₂, называемых фокусами, есть величина постоянная.

Фокусы F₁(c, 0) и F₂(–c, 0) построим, учитывая,

что (при а>b).

По определению сумма остается постоянной для любой точки М(х, у) эллипса.

Если центр симметрии эллипса расположен в точке С(х₀, у₀) и оси симметрии параллельны координатным осям, то уравнение эллипса:

(16)

В школьном курсе гипербола рассматривается как график обратной пропорциональной зависимости .

Рассмотрим более общий случай гиперболы, начав с ее определения:

Гиперболой называется множество точек плоскости, разность расстояний каждой из которых от двух данных точек есть величина постоянная. Простейшее (каноническое) уравнение гиперболы имеет вид:

(17)

Как видно, коэффициенты при х² и у² имеют разные знаки.

Числа а и b (а>0 и b>0) называются полуосями гиперболы.

Точки А₁(а,0), А₂(–а,0), В₁(0,b) и В₂(0,–b) называют вершинами гиперболы.

Построим прямоугольник со сторонами, проходящими через вершины А₁, А₂, В₁, В₂ параллельно координатным осям. Диагонали этого прямоугольника называют асимптотами гиперболы. Очевидно, уравнения асимптот

и

Через вершины А₁(а, 0) и А₂(-а, 0) проведем теперь две симметричные относительно координатных осей ветви гиперболы так, чтобы по мере удаления от центра симметрии – точки О(0,0) – они приближались бы к асимптотам, но не пересекали бы их.

Если же центр симметрии гиперболы расположен в точке С(х₀, у₀) и оси симметрии параллельны координатным осям, то уравнение гиперболы имеет вид:

,

Укажем, что гипербола является и графиком дробно-линейной функции .

Параболу в школьном курсе рассматривают как график квадратного трехчлена у=ах²+bх+с.

Выделяя из квадратного трехчлена полный квадрат, это уравнение легко привести к виду

(х–х₀)²=±2р×(у–у₀) (18)

Здесь точка С(х₀, у₀) – вершина параболы, ось симметрии параллельна Оу. Коэффициент р(р>0) называют параметром параболы. Знак плюс перед коэффициентом 2р соответствует параболе, ветви которой направлены вверх, знак минус – вниз.

Можно рассмотреть параболу с осью симметрией, параллельной оси Ох. Ее уравнение имеет вид

(у–у₀)² = ±2р × (х–х₀). (19)

Отметим, что уравнение параболы содержит квадрат только одной переменной: либо х (формула 18), либо у (формула 19).

Дадим определение, которое часто фигурирует как определение параболы.

Параболой называется множество точек плоскости, равноудаленных от данной прямой и от данной точки.

В заключение данного обзора кривых второго порядка отметим, что эти линии часто встречаются в различных вопросах естествознания. Например, движение материальной точки под воздействием центрального поля силы тяжести происходит по одной из этих линий.

Оптические свойства эллипса, гиперболы и параболы широко используется в инженерном деле. В частности, оптические свойства параболы используется при конструировании прожекторов, антенн, телескопов.

Такие термины, как «эллиптическая орбита», «эллипсоид инерции», «параболическая траектория», «параболическое зеркало» и т. д., убеждают в широком применении кривых второго порядка.

Вопросы для самоконтроля

Прежде чем Вы приступите к выполнению контрольного задания, попробуйте ответить на предлагаемые вопросы для самоконтроля. Если Вы будете испытывать затруднения при ответе на конкретный вопрос, попытайтесь найти на него ответ, вернувшись к теоретической части курса. Было бы лучше, если бы Вы воспользовались любым стандартным учебником по аналитической геометрии.

1. Что можно сказать о взаимном расположении векторов:

, ?

2. Как расположены векторы в декартовой системе координат на плоскости: ; ; ; ?

3. Среди векторов укажите равные векторы, коллинеарные векторы, векторы одинаковой длины, взаимно перпендикулярные векторы:

, , , .

4. Как найти точку пересечения двух линий на плоскости, если уравнения этих линий даны?

5. Каков геометрический смысл системы и ее решения?

6. Какое множество точек на плоскости определяется уравнением

1) х=2; 2) х+3=0; 3) у=–1;

4) у–3=0; 5) х+у=0; 6) у=|х| ?

7. Какое множество точек на плоскости определяется системой неравенств:

1) 2) ?

8. Какое множество точек в пространстве определяется уравнением:

1) х+у=1, 2) х=5 3) z=-2?

9. Какое множество точек в пространстве определяется системой неравенств:

?

2.10. Как выполнить контрольное задание № 2 «Элементы векторной алгебры и аналитической геометрии»

Задача № 1

Дан треугольник АВС:

А(4, 2), В(-2, 1), С(2, -3).

Найти длины и уравнения его сторон, угол при вершине B, площадь треугольника, уравнение описанной окружности. Записать систему неравенств, определяющих область треугольника.

При решении этой задачи будут использованы формулы, полученные в п. 4.

1) Найдем длины сторон по формуле

2) Составим уравнение каждой стороны треугольника по формуле (4):

Уравнение АВ: или у–1=

Уравнение ВС: или у–1= –(х + 2).

Уравнение АС: или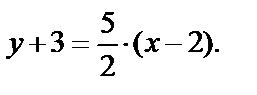

3) Для вычисления угла при вершине В найдем координаты векторов и , выходящих из точки В и совпадающих со сторонами треугольника:

;

Тогда величина искомого угла найдется из формулы:

.

4) Вычислим площадь треугольника по формуле (11):

Подставив координаты вершин А, В, С, получим:

S=14(кв. ед.).

Здесь определитель равен положительному числу 28, поэтому следует взять знак плюс.

5) Центр окружности, описанной около треугольника, лежит в точке пересечения серединных перпендикуляров к сторонам треугольника.

Найдем координаты середин двух сторон АВ и ВС и проведем через эти точки прямые, перпендикулярные сторонам треугольника.

Итак, пусть точка D – середина АВ.

Через точку D (1; ) проведем прямую с угловым коэффициентом k₂, который найдем из условия перпендикулярности прямых: k₂= – , где (см. уравнение АВ). k₂= – 8.

Уравнение перпендикуляра: у– = –8×(х–1) или 16х + 2у–19 = 0. Точка Е – середина ВС и ее координаты:

Через точку Е (0, –1) проведем прямую с угловым коэффициентом k=1, т. к. уравнение ВС: у–1=–(х+2).

Уравнение этого перпендикуляра: у+1=х или х–у–1=0.

Центр окружности (точку Р) найдем как точку пересечения найденных перпендикуляров из системы:

.

Тогда у = х – 1 = .

Точка Р ( – центр описанной окружности, радиус которой r = Найдем .

Уравнение описанной окружности –

или .

Составим систему неравенств, определяющих область треугольника АВС.

Уравнение прямой АВ: или х – 8у + 10 = 0.

Найдем ту полуплоскость с границей на прямой х – 8у + 10 = 0, в которой лежит вершина С(2, –3). Подставив ее координаты в левую часть уравнения прямой АВ, получим неравенство 2 – 8×(–3) + 10 < 0. Поэтому нужная нам полуплоскость определяется неравенством х – 8у + 10 < 0.

Уравнение прямой ВС: у – 1 = –(х + 2) или х + у + 1 = 0. Координаты точки А (4, 2) дают неравенство 4 + 2 + 1 > 0. Поэтому область треугольника лежит в полуплоскости, для которой х + у + 1 > 0.

Уравнение прямой АС: у + 3= или 5х – 2у – 16 = 0.

Координаты точки В (–2, 1) позволяют выбрать нужную полуплоскость:

, т.е. 5х – 2у – 16 < 0.

Система неравенств определяет область треугольника АВС.

Задача № 2.

Даны точки М₁(–1,2,0), М₂(1,–2,1), М₃(3,1,–1), М₄(3,0,1).

Составить уравнение плоскости, проходящей через

1) точки М₁, М₂, М₃;

2) точку М₄ параллельно плоскости М₁ М₂ М₃;

3) точку М₄ перпендикулярно вектору .

Вычислить объем пирамиды М₁М₂М₃М₄.

При решении этой задачи используются формулы из п. 6 и п. 7.

1) Составим уравнение плоскости, проходящей через три точки М₁, М₂, М₃ по формуле (13):

или 5х + 6у + 14z – 7 = 0.

Подставив координаты точек М₁, М₂, М₃ в полученное уравнение, убедимся, что уравнение составлено верно.

2) Коэффициенты при х, у, z в полученном уравнении (А=5; В=6; С=14) определяют положение параллельной плоскости, проходящей через точку (х₀, у₀, z₀) по формуле (7):

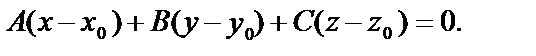
Уравнение плоскости, проходящей через точку М₄(3,0,1) параллельно плоскости М₁М₂М₃ имеет вид:

или 5х + 6у + 14z – 29 = 0.

3) Принимая вектор за нормальный вектор плоскости, составим уравнение плоскости, проходящей через точку М₄ (3,0,1) перпендикулярно вектору :

2×(х–3)–4(у–0) + 1×(z–1) = 0 или 2х–4у + z– 7 = 0.

4) Объем пирамиды М₁М₂М₃М₄ вычислим, используя формулу (12):

.

V= (куб. ед.).

Задача № 3.

Какую линию определяет уравнение?

а) Дано уравнение:

16х² + 25у² – 96х + 50у – 231 = 0.

Приведем его к простейшему виду, выделив полные квадраты с переменной х и с переменной у:

16×(х² – 6х + 9) – 16×9 + 25×(у² + 2у + 1) – 25 – 231 = 0.

16×(х – 3)² + 25×(у + 1)² = 400.

Разделим обе части на 400:

или .

Получено уравнение эллипса (16) с полуосями а=5, b=4 и центром симметрии в точке С(3,–1).

Построим эллипс, оси симметрии которого проходят через точку С(3,–1) параллельно координатным осям. Их уравнения х = 3 и у = –1.

б) Дано уравнение:

9х² + 4у² + 18х – 16у – 11 = 0.

Преобразуем его:

9(х² + 2х + 1) – 9 + 4(у² – 4у + 4) – 16 – 11 = 0

9(х + 1)² + 4(у – 2)² = 36

.

Это уравнение эллипса с центром симметрии в точке С(–1,2). Оси симметрии имеют уравнения: х = –1 и у = 2.

Полуоси эллипса а = 2 и b = 3, т. е. эллипс вытянут по оси Оу.