
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Образец решения задач из контрольного задания
Задача № 1. Проверить, являются ли указанные функции решениями данного уравнения


Решение.
а) 
Подставим  в уравнение:
в уравнение:
 или
или
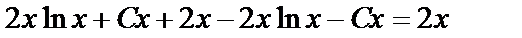 — верно, т.е.
— верно, т.е.  — решение уравнения.
— решение уравнения.
б) 
 или
или
 — неверно, т.е.
— неверно, т.е.  не является решением.
не является решением.
в) 
 или
или
 — верно, т.е.
— верно, т.е.  — решениеуравнения.
— решениеуравнения.
Задача № 2. Проверить, является ли функция  общим решением уравнения
общим решением уравнения  и найти частное решение этого уравнения, удовлетворяющее начальному условию:
и найти частное решение этого уравнения, удовлетворяющее начальному условию:
 .
.
Решение. Подставим функцию 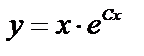 в данное уравнение:
в данное уравнение:

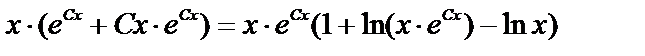

Так как получено верное равенство, то функция 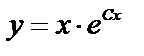 , зависящая от произвольной постоянной С, действительно является общим решением уравнения.
, зависящая от произвольной постоянной С, действительно является общим решением уравнения.
Подставим начальные условия  в общее решение:
в общее решение:
 Найденное значение С подставим в общее решение:
Найденное значение С подставим в общее решение:
 — частное решение.
— частное решение.
Задача № 3. Найти общее решение дифференциального уравнения (или частное решение, удовлетворяющее данному начальному условию).
а) 
б) 
в)  .
.
Дата добавления: 2015-01-05; просмотров: 254; Мы поможем в написании вашей работы!; Нарушение авторских прав |