
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Метод неопределённых коэффициентов
Пусть правая часть  уравнения
уравнения  (3)
(3)
представляет собой произведение показательной функции (экспоненты) на многочлен, т.е.
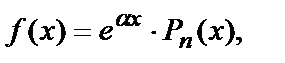
где a — действительное число,  — многочлен степени n. Тогда возможны следующие случаи:
— многочлен степени n. Тогда возможны следующие случаи:
1) Число a не является корнем характеристического уравнения
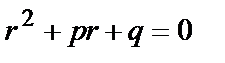 (2).
(2).
В этом случае частное решение нужно искать в виде
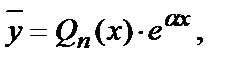
где 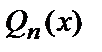 - многочлен той же степени n, что и
- многочлен той же степени n, что и  но с неопределёнными коэффициентами.
но с неопределёнными коэффициентами.
2) Число a есть простой (однократный) корень характеристического уравнения.
В этом случае частное решение нужно искать в виде
 .
.
3) Число a есть двукратный корень характеристического уравнения.
В этом случае частное решение нужно искать в виде

Неизвестные коэффициенты многочлена 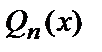 найдём из условия, что функция
найдём из условия, что функция  является решением уравнения (3), т.е. удовлетворяет этому уравнению.
является решением уравнения (3), т.е. удовлетворяет этому уравнению.
Рассмотрим примеры, на которых покажем не только принцип применения метода, но и порядок оформления решения.
№ 16. Найти общее решение уравнения

1) Составим характеристическое уравнение и найдём его корни:



2) Запишем общее решение однородного уравнение:

3) Запишем, в каком виде следует искать частное решение  данного уравнения. Для этого выпишем правую часть его
данного уравнения. Для этого выпишем правую часть его  и сравним с
и сравним с 
Многочлен  второй степени (n=2) c коэффициентами 25, 0, -2
второй степени (n=2) c коэффициентами 25, 0, -2  Показательная функция
Показательная функция  в нашем случае, т.е. a=0. Т.к. a=0 не совпадает ни с одним из корней характеристического уравнения
в нашем случае, т.е. a=0. Т.к. a=0 не совпадает ни с одним из корней характеристического уравнения  то частное решение нужно искать в виде:
то частное решение нужно искать в виде:
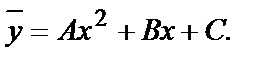
Многочлен 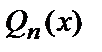 в нашем случае второй степени (n=2), неизвестные коэффициенты А, В, С этого многочлена нужно найти, подставив
в нашем случае второй степени (n=2), неизвестные коэффициенты А, В, С этого многочлена нужно найти, подставив  в данное уравнение:
в данное уравнение:
4) Запишем 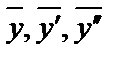 столбиком:
столбиком:

|
Слева укажем коэффициенты 5; 6; 1, на которые следует умножить  чтобы получить левую часть уравнения
чтобы получить левую часть уравнения  Понятно, что в левой части мы получим многочлен второй степени, который должен быть равен многочлену второй степени в правой части. Многочлены будут равны тогда и только тогда, когда равны коэффициенты при одинаковых степенях х. Запишем столбиком полученные уравнения:
Понятно, что в левой части мы получим многочлен второй степени, который должен быть равен многочлену второй степени в правой части. Многочлены будут равны тогда и только тогда, когда равны коэффициенты при одинаковых степенях х. Запишем столбиком полученные уравнения:
| х2 х1 х0 | 
| } |
Мы получили систему трёх уравнений с тремя неизвестными коэффициентами А, В, С. Решив её, найдём: А=5, В=-12, С=12.
Частное решение 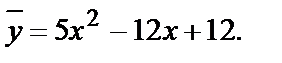
5) Общее решение данного уравнения
 или
или

№ 17. 
1) 
2) 
3) Сравним правую часть данного уравнения 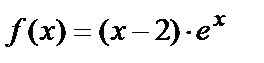 с
с 
Отмечаем, что a=1 совпадает с одним корнем характеристического уравнения и многочлен х–2 степени n = 1. Поэтому частное решение следует искать в виде 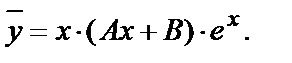
4) Так как требуется найти  то удобнее записать
то удобнее записать  в виде
в виде
 .
.
Запишем 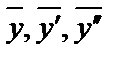 столбиком:
столбиком:
| -7 | 
|
Каждое слагаемое левой части уравнения и правая часть содержат общий множитель 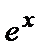 . Предполагая, что на
. Предполагая, что на 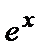 можно разделить уравнение, приравняем коэффициенты при одинаковых степенях х слева и справа. Заметим прежде, что в левой части уравнения взаимно уничтожаются слагаемые с
можно разделить уравнение, приравняем коэффициенты при одинаковых степенях х слева и справа. Заметим прежде, что в левой части уравнения взаимно уничтожаются слагаемые с  (они подчёркнуты).
(они подчёркнуты).
В оставшихся трёх слагаемых наивысшая степень х — первая.
Получим систему из двух уравнений:
 х
х0 х
х0 
| –14А+4А=1 –7В+2А+2В= –2 | } |  ; ; 
|

5) Общее решение

6.6. Пусть правая часть  неоднородного Д.У.-II представляет собой сумму функций вида
неоднородного Д.У.-II представляет собой сумму функций вида 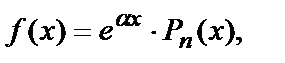 т.е.
т.е.

Частное решение  этого уравнения следует искать в виде суммы
этого уравнения следует искать в виде суммы  частных решений двух уравнений
частных решений двух уравнений
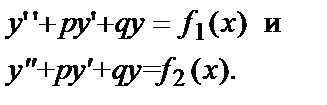
№ 18. Найдём общее решение уравнения
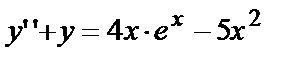
Здесь 

1) 
2) 
3) при 

|
| х х0 | А+А=4 В+2А+В=0 |
А=2; В=-2.

4) при 
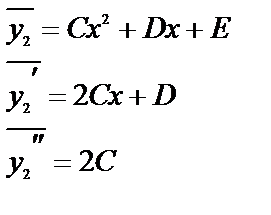
|
| x2 x1 x0 | C=-5 D=0 E+2C=0 |
C= –5; Е=10.

5) Общее решение данного уравнения  или
или

Прежде чем Вы приступите к решению контрольного задания, попытайтесь ответить на предлагаемые вопросы для самоконтроля. Если Вы будете испытывать затруднения при ответе на конкретный вопрос, попытайтесь найти на него ответ, вернувшись к теоретической части курса.
Вопросы для самоконтроля
1) Какое уравнение называется дифференциальным ?
2) Что называется решением Д.У.? Сколько решений имеет Д.У.?
3) Как установить, является ли данная функция решением данного Д.У.?
4) Какое Д.У. называется дифференциальным уравнением первого порядка (Д.У.-I)?
5) В каком виде можно записать Д.У.-I?
6) Что называется общим решением Д.У.-I?
7) Как найти частное решение Д.У.-I, удовлетворяющее заданному начальному условию?
8) Какое Д.У.-I называется уравнением с разделёнными переменными?
9) Как установить, является ли данное Д.У.-I уравнением с разделяющимися переменными? Каково правило разделения переменных?
10) Какое Д.У.-I называется однородным?
11) Как проверить, является ли Д.У.-I однородным?
12) Каким способом решается однородное Д.У.-I?
13) Какое Д.У.-I называется линейным?
14) Каков способ решения линейного Д.У.-I?
15) Какой вид может иметь дифференциальное уравнение второго порядка (Д.У.-II)?
16) Что называется общим решением Д.У.-II?
17) Как найти частное решение Д.У.-II, удовлетворяющее заданным начальным условиям?
18) Какие Д.У.-II допускают понижение порядка? Как они решаются?
19) Какое Д.У.-II называют линейным?
20) Какой вид имеет однородное линейное Д.У.-II с постоянными коэффициентами?
21) Какое уравнение называется характеристическим? Что оно собой представляет?
22) Какие случаи рассматриваются при отыскании общего решения однородного линейного Д.У.-II с постоянными коэффициентами? Какой вид имеет его общее решение в каждом из этих случаев?
23) Какой вид имеет неоднородное линейное Д.У.-II?
24) Какова структура общего решения неоднородного линейного Д.У.-II с постоянными коэффициентами?
25) Для какого вида правой части можно применить метод неопределенных коэффициентов? Как составить вид частного решения и от чего зависит этот вид?
Ответы на предложенные вопросы Вы найдёте в настоящем курсе.
| Номер вопроса | Где найти ответ |
| 1, 2, 3 4, 5, 6, 7 8,9 10, 11, 12 13,14 15, 16, 17 20, 21, 22 23, 24 | П. 5.1 П. 5.2 П. 5.3 П. 5.3 П. 5.3 П. 5.4 П. 5.5 П. 5.6 П. 5.6 П. 5.6 П. 5.6 |
Дата добавления: 2015-01-05; просмотров: 353; Мы поможем в написании вашей работы!; Нарушение авторских прав |