
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Решение. а) . Это дифференциальное уравнение является линейным, но проще решать его как уравнение с разделяющимися переменными:
а)  . Это дифференциальное уравнение является линейным, но проще решать его как уравнение с разделяющимися переменными:
. Это дифференциальное уравнение является линейным, но проще решать его как уравнение с разделяющимися переменными:
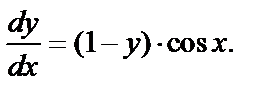 Умножим на
Умножим на 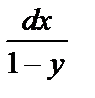 .
. 
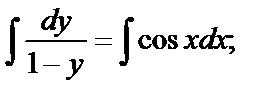
 или
или

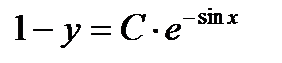
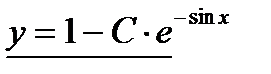 — общее решение.
— общее решение.
Проверка:
 Подставим в уравнение
Подставим в уравнение  ;
;  — верно.
— верно.
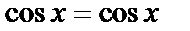 .
.
б)  . Это однородное Д.У.-I, т.к. после замены х на tx; у на ty уравнение не изменится:
. Это однородное Д.У.-I, т.к. после замены х на tx; у на ty уравнение не изменится:
 (разделить на t).
(разделить на t).
Решаем подстановкой 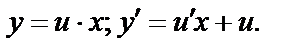
 или
или 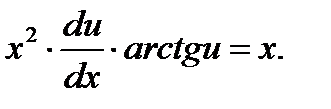
Умножим на 
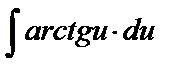 по частям
по частям 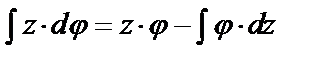 — формула интегрирования по частям.
— формула интегрирования по частям.


Интегрируя обе части уравнения 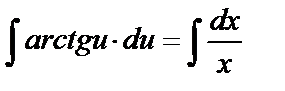 , получим
, получим
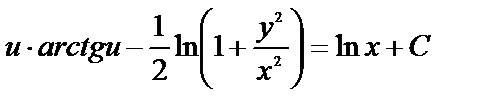 . Подставим
. Подставим  или
или 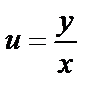 :
:  — общий интеграл.
— общий интеграл.
Подставим начальное условие: 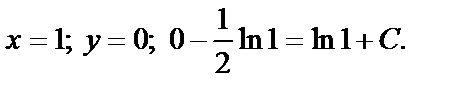
Отсюда С=0.
Искомый частный интеграл 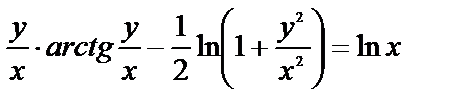 или
или
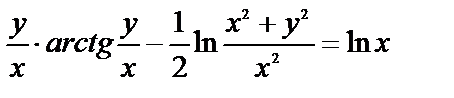
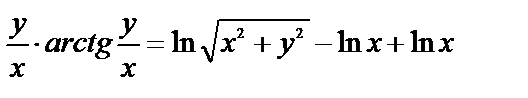
 .
.
Проверка: продифференцируем по х обе части последнего равенства:
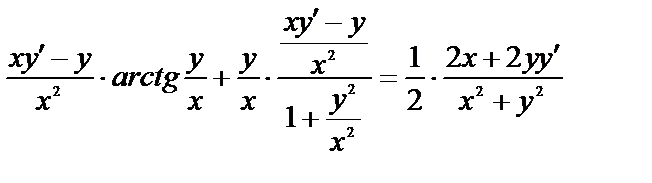
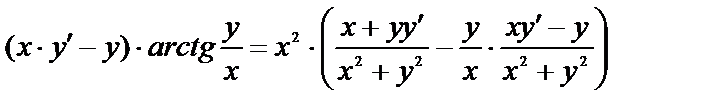
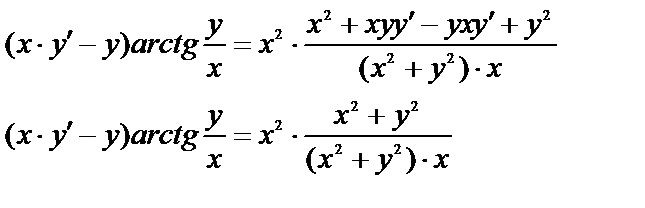
или 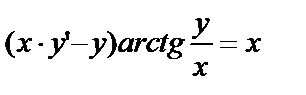 - получено данное уравнение, т.е. частное решение найдено правильно.
- получено данное уравнение, т.е. частное решение найдено правильно.
в) 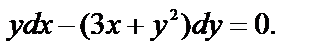 Это уравнение линейно относительно
Это уравнение линейно относительно 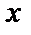 и
и 

Дата добавления: 2015-01-05; просмотров: 250; Мы поможем в написании вашей работы!; Нарушение авторских прав |