Линейные неоднородные дифференциальные уравнения второго порядка и их решение

Линейное неоднородное уравнение отличается от однородного уравнения функцией в правой части.

Будем придерживаться нумерации:

— однородное уравнение (1)

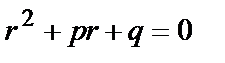- характеристическое уравнение (2)

- неоднородное уравнение (3).

Существует теорема о структуре общего решения неоднородного уравнения (3), согласно которой

общее решение неоднородного линейного дифференциального уравнения равно сумме какого-либо частного решения этого уравнения и общего решения соответствующего однородного уравнения.

Пусть у — общее решение уравнения

(3),

— его частное решение;

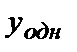- общее решение однородного уравнения

Тогда

Таким образом, основная задача при решении неоднородного уравнения состоит в нахождении какого-либо его частного решения.

Укажем один из методов нахождения частных решений неоднородного уравнения.