
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Обратимся к решению квадратных уравнений

Формула корней квадратного уравнения  где
где  - дискриминант.
- дискриминант.
Любое квадратное уравнение всегда имеет два корня (это известное положение высшей алгебры).
1) Если  то
то  и
и  — два различных действительных корня (числа
— два различных действительных корня (числа  являются действительными или вещественными) .
являются действительными или вещественными) .
2) Если Д=0, то х1=х2=  — два равных действительных корня.
— два равных действительных корня.
3) Если Д<0, то квадратное уравнение имеет два корня, но они не являются действительными числами. Корни эти называются комплексными числами.
Обозначим  и назовём мнимой единицей (
и назовём мнимой единицей (  ). Тогда число вида
). Тогда число вида  где
где 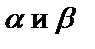 - любые действительные числа, назовём комплексным числом. Здесь
- любые действительные числа, назовём комплексным числом. Здесь  называют действительной частью комплексного числа,
называют действительной частью комплексного числа,  называют мнимой частью,
называют мнимой частью,  - коэффициентом мнимой части комплексного числа.
- коэффициентом мнимой части комплексного числа.
Для всякого комплексного числа  существует комплексное число, ему сопряжённое
существует комплексное число, ему сопряжённое  Так, для числа
Так, для числа  сопряжённым является
сопряжённым является 
Два комплексных числа  и
и  являются взаимно-сопряжёнными. Покажем примеры решения квадратных уравнений.
являются взаимно-сопряжёнными. Покажем примеры решения квадратных уравнений.
1) 



2) 


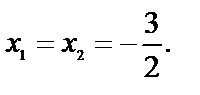
3) 


4) 



5) 




Получена пара взаимно–сопряжённых комплексных чисел с действительной частью  и коэффициентом мнимой части
и коэффициентом мнимой части 
6) 



Получена пара взаимно-сопряжённых комплексных чисел  где
где 
Заметим, что всякое алгебраическое уравнение степени n имеет ровно n корней, среди которых могут быть как действительные (различные или равные), так и комплексные (обязательно попарно взаимно–сопряжённые).
Для решения уравнения  разложим левую его часть на множители:
разложим левую его часть на множители:  Остаётся решить три простейших уравнения:
Остаётся решить три простейших уравнения: 
Имеем четыре корня:

Для решения уравнения 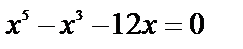 разложим левую его часть на множители:
разложим левую его часть на множители:
 и решим два уравнения
и решим два уравнения 
В уравнении  сделаем замену
сделаем замену  и получим
и получим 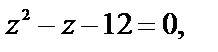 корни которого
корни которого  или
или 
Два последних уравнения позволяют найти корни 
Учитывая найденный уже корень  имеем пять корней, из которых два
имеем пять корней, из которых два  - взаимно–сопряжённые комплексные числа.
- взаимно–сопряжённые комплексные числа.
Дата добавления: 2015-01-05; просмотров: 276; Мы поможем в написании вашей работы!; Нарушение авторских прав |