
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Линейные дифференциальные уравнения первого порядка
Были рассмотрены дифференциальные уравнения первого порядка с разделяющимися переменными и однородные и указаны способы их решения. Рассмотрим линейные дифференциальные уравнения первого порядка и приводящиеся к ним.
Определение. Дифференциальное уравнение называется линейным, если оно линейно относительно искомой функции и её производной.
Общий вид линейного Д.У.-I таков:
 где
где  и
и  - непрерывные функции или постоянные. Если
- непрерывные функции или постоянные. Если  то уравнение
то уравнение  решается как уравнение с разделяющимися переменными.
решается как уравнение с разделяющимися переменными.
Рассмотрим уравнения:
1)  Это уравнение является линейным по определению, но лучше рассматривать его как уравнение с разделяющимися переменными:
Это уравнение является линейным по определению, но лучше рассматривать его как уравнение с разделяющимися переменными: 
2) 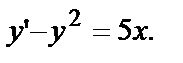 Это уравнение не является линейным, т.к. функция у присутствует в уравнении не в первой степени.
Это уравнение не является линейным, т.к. функция у присутствует в уравнении не в первой степени.
3)  Это уравнение является линейным по определению, но проще рассматривать его как однородное Д.У.-I.
Это уравнение является линейным по определению, но проще рассматривать его как однородное Д.У.-I.
4) 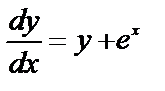 . Это уравнение является линейным. Записав его в виде
. Это уравнение является линейным. Записав его в виде  получим
получим 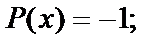

Способ решения линейного Д.У.-I: подстановка  где
где 
 — вспомогательные функции.
— вспомогательные функции.
Покажем на примере, что любую функцию 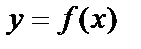 можно представить в виде произведения двух функций, одна из которых выбирается произвольно, а вторая зависит от этого выбора.
можно представить в виде произведения двух функций, одна из которых выбирается произвольно, а вторая зависит от этого выбора.
Пусть  Можно
Можно 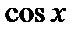 представить в виде различных пар сомножителей:
представить в виде различных пар сомножителей:

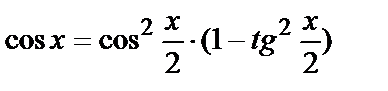
 где первый множитель
где первый множитель  выбирается произвольно.
выбирается произвольно.
Указанная подстановка  приводит линейное Д.У.-I к решению двух Д.У. с разделяющимися переменными. Покажем это в общем виде.
приводит линейное Д.У.-I к решению двух Д.У. с разделяющимися переменными. Покажем это в общем виде.
В линейное уравнение
 подставим
подставим 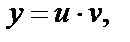


(1) 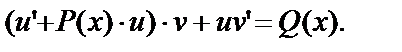 В этом уравнении потребуем, чтобы
В этом уравнении потребуем, чтобы
(2) 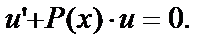 Тем самым мы выбираем множитель
Тем самым мы выбираем множитель 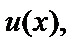 причём без учёта произвольной постоянной.
причём без учёта произвольной постоянной.
Решив (2) – Д.У. с разделяющимися переменными, подставим найденную функцию 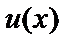 в уравнение (1) и получим
в уравнение (1) и получим
(3) 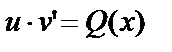 уравнение с разделяющимися переменными. Его общее решение позволит получить второй множитель
уравнение с разделяющимися переменными. Его общее решение позволит получить второй множитель  Тогда
Тогда  — общее решение линейного Д.У.-I.
— общее решение линейного Д.У.-I.
№9. Найдём общий интеграл уравнения 


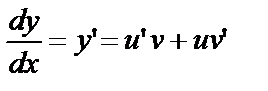

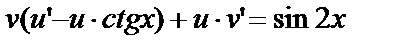 (1)
(1)
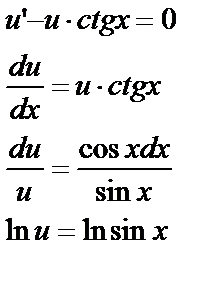
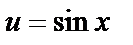 подставим в (1) подставим в (1)
| 
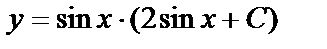 — общий интеграл. — общий интеграл.
|
Проверка. Запишем общий интеграл в виде: 
 Подставим в данное уравнение:
Подставим в данное уравнение: 
№10. Найти частное решение Д.У.
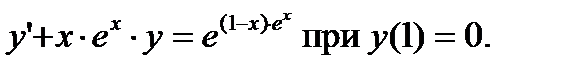
Данное линейное Д.У.-I решаем подстановкой
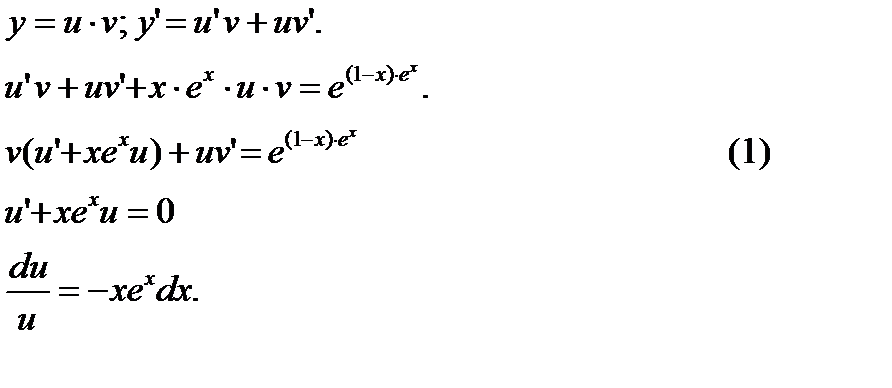
Рассмотрим вначале
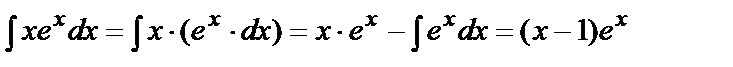
Первый множитель 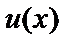 получим из равенства
получим из равенства  или
или 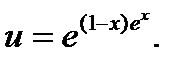 Эту функцию подставим в уравнение (1):
Эту функцию подставим в уравнение (1):
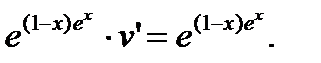 Сократив обе части уравнения, получим
Сократив обе части уравнения, получим 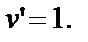 Отсюда
Отсюда 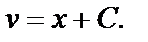
Общее решение данного Д.У. 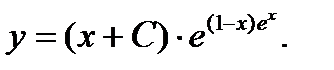
Используя начальные условия у=0 при х=1, имеем  Частное решение данного дифференциального уравнения
Частное решение данного дифференциального уравнения 
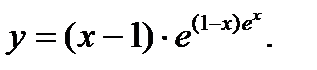
Попробуйте доказать правильность решения.
№11. Найти общее решение уравнения  В таком виде данное уравнение нельзя решить известными нам способами. Запишем уравнение в виде
В таком виде данное уравнение нельзя решить известными нам способами. Запишем уравнение в виде 
Если в последнем уравнении считать x функцией от у, то уравнение – линейное относительно функции  Итак, решаем линейное Д.У.
Итак, решаем линейное Д.У. 


 (1)
(1)
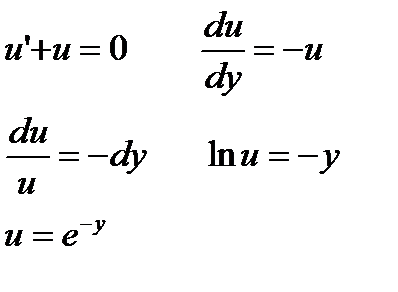
|  
|
Искомое решение

Замечание. Напомним, как следует искать 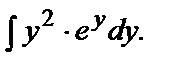 Применяя формулу интегрирования по частям
Применяя формулу интегрирования по частям
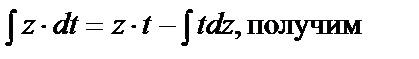


Уравнения, приводящиеся к линейным (уравнения Бернулли)
Уравнение вида

называется уравнением Бернулли.
Здесь 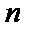 - действительное число, причём при
- действительное число, причём при 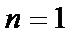 получим уравнение с разделяющимися переменными, при
получим уравнение с разделяющимися переменными, при 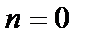 получим линейное уравнение. При
получим линейное уравнение. При  уравнение Бернулли приводится к линейному, решается как и линейное подстановкой
уравнение Бернулли приводится к линейному, решается как и линейное подстановкой  Рассмотрим на примере:
Рассмотрим на примере:
№11.  Определим тип этого уравнения. Легко увидеть, что переменные разделить нельзя:
Определим тип этого уравнения. Легко увидеть, что переменные разделить нельзя:  не представить в виде нужных нам множителей. Однородным это уравнение не является, т.к. из скобки
не представить в виде нужных нам множителей. Однородным это уравнение не является, т.к. из скобки  не удаётся вынести
не удаётся вынести  после соответствующей замены
после соответствующей замены 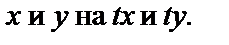 Линейным это уравнение не является, т.к. содержит
Линейным это уравнение не является, т.к. содержит 
Представим это уравнение в виде:
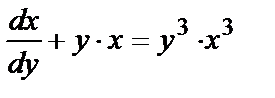 и можно утверждать, что это уравнение имеет общий вид
и можно утверждать, что это уравнение имеет общий вид  т.е. является уравнением Бернулли относительно функции
т.е. является уравнением Бернулли относительно функции 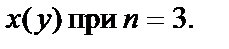 Решаем его подстановкой
Решаем его подстановкой  — вспомогательные функции. Подставим
— вспомогательные функции. Подставим 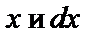 в исходное уравнение
в исходное уравнение 

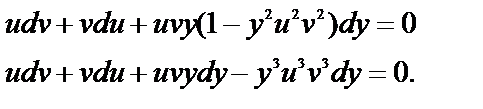
Сгруппируем слагаемые, содержащие v (только в первой степени!):

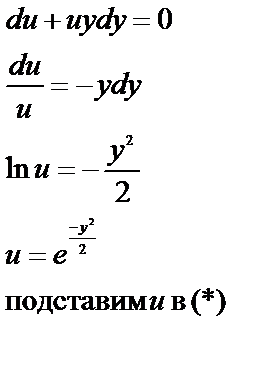
| 
|
Для получения общего интеграла найдём 
 или
или
 - общий интеграл.
- общий интеграл.
Подставим начальное условие 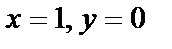 и найдём С:
и найдём С:

Частный интеграл имеет вид

Заметим, что неопределённый интеграл  вычислен с применением формулы интегрирования по частям
вычислен с применением формулы интегрирования по частям 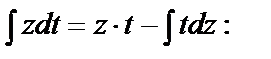



| 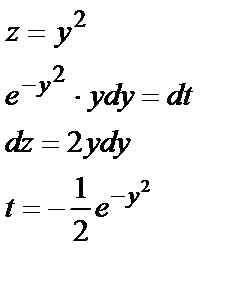
|
Дата добавления: 2015-01-05; просмотров: 318; Мы поможем в написании вашей работы!; Нарушение авторских прав |