Дифференциальные уравнения первого порядка. Так как дифференциальное уравнение первого порядка (условимся в дальнейшем писать Д.У

Так как дифференциальное уравнение первого порядка (условимся в дальнейшем писать Д.У. — I) содержит независимую переменную х, функцию у и её производную 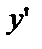, то общий вид Д.У. – I

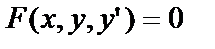(1)

Если уравнение (1) решить относительно производной то оно может быть записано в виде

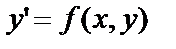(2)

Так как 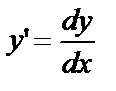, то из (2)

можно перейти к форме

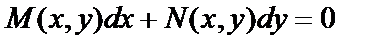(3)

Например, Д.У. 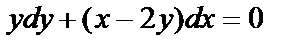(3)

можно записать в виде 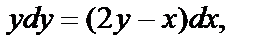разделив обе части последнего уравнения на . Получим

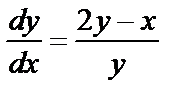или (2)

Наконец, можно получить

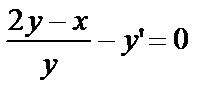(1)

Таким образом, формы (1), (2), (3) совершенно равноправны, можно пользоваться любой из удобных для решения.

Определение. Общим решением дифференциального уравнения первого порядка (Д.У. — I) называется функция 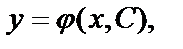которая зависит от одной произвольной постоянной С и

1) удовлетворяет данному Д.У. – I при любом значении С;

2) каково бы ни было начальное условие y(x₀)=y₀, можно найти такое значение С₀, при котором функция удовлетворяет начальному условию.

Например, для Д.У. – I общим решением является функция 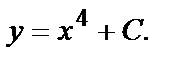Найдём частное решение, удовлетворяющее начальному условию 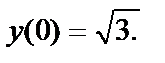Для этого подставим в общее решение 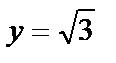и х = 0. Получим — уравнение для опредления постоянной 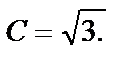Теперь подставим в общее решение. Функция 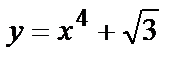и будет искомым частным решением.