
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Основные свойства определенного интеграла
1.
2. 
Эти свойства аналогичны соответствующим свойствам неопределенного интеграла.
Следующее важное свойство определенного интеграла часто используется в приложениях.
3. 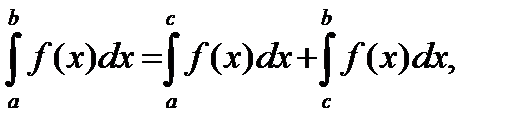
где  любая точка из
любая точка из 
Это свойство имеет простой геометрический смысл: если  на
на 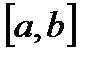 и
и  то оно утверждает, что площадь
то оно утверждает, что площадь  криволинейной трапеции, заштрихованной на рис. 4, равна сумме
криволинейной трапеции, заштрихованной на рис. 4, равна сумме  площадей составляющих ее меньших криволинейных трапеций.
площадей составляющих ее меньших криволинейных трапеций.

4. Если функция  непрерывна на отрезке
непрерывна на отрезке  то существует такая точка с из
то существует такая точка с из 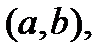 что
что


Геометрически это означает, что между  и
и 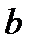 существует такая точка
существует такая точка  что площадь криволинейной трапеции (рис. 5) равна площади прямоугольника, основанием которого является отрезок
что площадь криволинейной трапеции (рис. 5) равна площади прямоугольника, основанием которого является отрезок  а высотой -
а высотой - 
Рис. 5
5. Если  на
на  то
то

6. Если 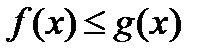 на
на  то
то

Это свойство тоже имеет простой геометрический смысл: если  на
на  то площадь меньшей криволинейной трапеции
то площадь меньшей криволинейной трапеции  (рис. 6) меньше площади большей криволинейной трапеции
(рис. 6) меньше площади большей криволинейной трапеции 

7. Если  на
на  то
то


Это свойство тоже легко проиллюстрировать геометрически: если 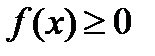 на
на 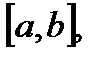 то оно утверждает, что площадь криволинейной трапеции больше площади прямоугольника
то оно утверждает, что площадь криволинейной трапеции больше площади прямоугольника  (рис. 7) и меньше площади прямоугольника
(рис. 7) и меньше площади прямоугольника 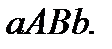
Рис. 7.
Дата добавления: 2015-01-05; просмотров: 267; Мы поможем в написании вашей работы!; Нарушение авторских прав |