
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
ТЕМА 5. ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
Решение многих задач естествознания, техники, экономики приводится к нахождению неизвестных функций, описывающих рассматриваемые явления или процессы, когда известны соотношения, связывающие между собой эти функции и их производные. Такие соотношения называются дифференциальными уравнениями. Рассмотрим конкретную задачу о потоке научной информации.
Задача. При исследовании роста информационных потоков в науке (числа научных публикаций) исходят из допущения, что скорость роста 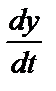 пропорциональна достигнутому уровню у числа публикаций, иначе говоря
пропорциональна достигнутому уровню у числа публикаций, иначе говоря 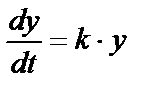 (k>0), где k – константа, характеризующая отклики на публикации в той или иной области знания.
(k>0), где k – константа, характеризующая отклики на публикации в той или иной области знания.
Решение этого дифференциального уравнения имеет вид экспоненты
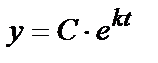
Здесь С – постоянная, характеризующая некоторый начальный уровень науки.
Интересно отметить, что относительной скорости роста в 7% (k=0,07) соответствует удвоение уровня примерно за 10 лет. Действительно, если в начальный момент t=0 уровень y0=C, точерез время Т (при t=T) , будет достигнут уровень 2y0:
2y0=С 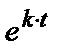 (T – в годах)
(T – в годах)
Мы полагаем  , тогда
, тогда
2=  . Логарифмируя, находим
. Логарифмируя, находим  . Отсюда
. Отсюда
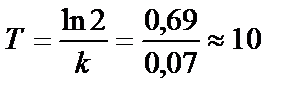 (лет).
(лет).
В рассмотренной задаче было составлено дифференциальное уравнение и приведено его решение. Вам предлагается изучить простейшие дифференциальные уравнения, их виды, способы их решения.
Предложенная тема является логическим продолжением уже рассмотренных положений дифференциального и интегрального исчислений. Успешное изучение темы напрямую зависит от приобретённых Вами навыков дифференцирования и интегрирования.
Основные понятия и определения
Определение. Дифференциальным уравнением называется уравнение, связывающее независимую переменную х, искомую функцию у=f(x) и её производные различных порядков.
Например:
1) 
2) 
3) 
Последнее уравнение можно записать в виде:  или
или
 или
или 
т.е. дифференциальное уравнение может содержать производные (  или
или  ) или дифференциалы dx и dy независимой перменной и функции.
) или дифференциалы dx и dy независимой перменной и функции.
Определение. Порядком дифференциального уравнения называется порядок наивысшей производной, входящей в уравнение. Так, в рассмотренных примерах первое уравнение – второго порядка, второе и третье – первого порядка.
Определение. Решением дифференциального уравнения называется любая функция y=f(x), удовлетворяющая этому уравнению.
Пример. Показать, что функция 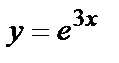 является решением уравнения
является решением уравнения 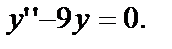
Решение. Для функции 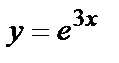 находим первую производную
находим первую производную  и второю производную
и второю производную 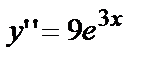 . Подставляя y и
. Подставляя y и  в уравнение, получим тождество
в уравнение, получим тождество  что и доказывает, что функция
что и доказывает, что функция 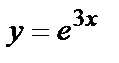 - решение уравнения
- решение уравнения 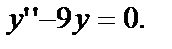
Пример. Укажите, какая из функций
1) 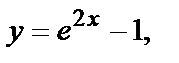 2)
2)  3)
3) 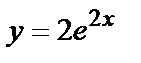
является решением уравнения 
Решение: 1) 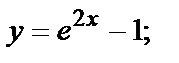

 . Подставляя в данное уравнение, получим:
. Подставляя в данное уравнение, получим: 
Функция  не является решением.
не является решением.
2) 
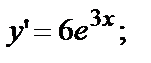

Подставляя в данное уравнение, получим: 
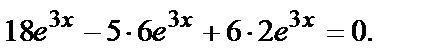 Функция
Функция  - решение данного уравнения.
- решение данного уравнения.
3) 


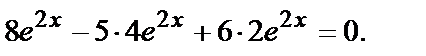
Функция 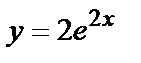 - решение данного уравнения.
- решение данного уравнения.
Замечание. Легко видеть, что функции вида 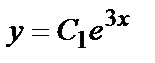 и
и 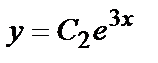 при произвольных постоянных С1 и С2 также являются решениями данного уравнения.
при произвольных постоянных С1 и С2 также являются решениями данного уравнения.
Пример. Легко убедиться, что функция  - решение уравнения
- решение уравнения 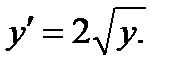 Аналогично, и функции
Аналогично, и функции 

 и вообще любая функция вида
и вообще любая функция вида  где С – произвольная постоянная, также является решением уравнения
где С – произвольная постоянная, также является решением уравнения 
Итак, дифференциальному уравнению удовлетворяет целая система функций. Для выделения одной из них должны быть заданы так называемые начальные условия, т.е. известное значение функции y=y0 при заданном значении независимой переменной х=х0. Начальные условия записываются в виде:
y=y0 при х=х0; или y(x0)=y0; или  .
.
Определение. Решение y=j(x) дифференциального уравнения, удовлетворяющее начальным условиям y(x0)=y0, называется частным решением дифференциального уравнения.
Например, для уравнения 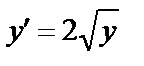 при начальных условиях y(3)=1из функции
при начальных условиях y(3)=1из функции 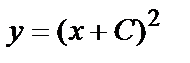 выделим соответсвующее частное решение. Для этого в решение
выделим соответсвующее частное решение. Для этого в решение 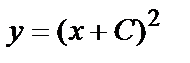 подставим у=1 и х=3. получим уравнение 1=(3+С)2 для вычисления постоянной С. В нашем случае С= –2. Подставив найденное
подставим у=1 и х=3. получим уравнение 1=(3+С)2 для вычисления постоянной С. В нашем случае С= –2. Подставив найденное
С= –2 в решение 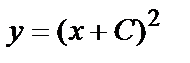 , получим
, получим 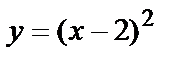 - искомое частное решение.
- искомое частное решение.
Рассмотрим некоторые методы решения дифференциальных уравнений.
Дата добавления: 2015-01-05; просмотров: 275; Мы поможем в написании вашей работы!; Нарушение авторских прав |