
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Однородные дифференциальные уравнения первого порядка
Легко можно убедиться в том, что дифференциальные уравнения



не являются уравнениями с разделяющимися переменными. Их называют однородными Д.У. – I.
Определение. Дифференциальное уравнение 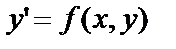 называется однородным дифференциальным уравнением первого порядка, если
называется однородным дифференциальным уравнением первого порядка, если  - однородная функция нулевого измерения.
- однородная функция нулевого измерения.
Замечание.  назовём однородной функцией нулевого измерения, если
назовём однородной функцией нулевого измерения, если 
Так, функции 
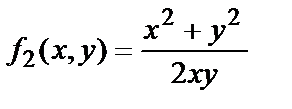 — однородные функции нулевого измерения, т.к.
— однородные функции нулевого измерения, т.к.


Чтобы проверить, является ли Д.У. однородным, нужно заменить в этом уравнении х на tx, y на ty. Если после этого t всюду сократится и получится первоначальное уравнение, то данное уравнение — однородное.
Поэтому Д.У.  является однородным.
является однородным.

Разделив на t, получим исходное уравнение.
Способ решения однородного Д.У. – I укажем без доказательства.
Однородное дифференциальное уравнение первого порядка приводится к уравнению с разделяющимися переменными подстановкой  (или
(или 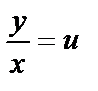 ), где u – некоторая функция х.
), где u – некоторая функция х.
Решим уравнения.
№7. Найти общее решение Д.У.  Решаем подстановкой
Решаем подстановкой 
 Подставив y и
Подставив y и 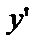 в данное уравнение, получим
в данное уравнение, получим  или
или 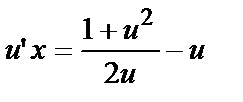 — Д.У. с разделяющимися переменными относительно вспомогательной функции u. Упростим правую часть:
— Д.У. с разделяющимися переменными относительно вспомогательной функции u. Упростим правую часть:  Умножив на
Умножив на  получим уравнение с разделёнными переменными
получим уравнение с разделёнными переменными 
Интегрируя, получим

Подставив  получим общий интеграл данного Д.У.:
получим общий интеграл данного Д.У.:
 или
или 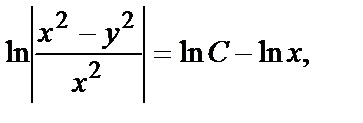

Отсюда:  - общий интеграл в более простой форме.
- общий интеграл в более простой форме.
Проверка:
| { | 
|
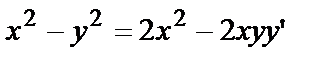 или
или 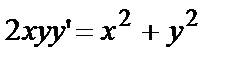
 — исходное уравнение.
— исходное уравнение.
№8. Найти частное решение Д.У.
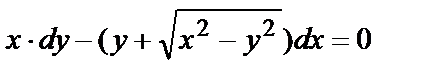 при у(1)=p.
при у(1)=p.
Подставив вместо х и у соответственно  и
и  , убедимся, что данное Д.У. является однородным:
, убедимся, что данное Д.У. является однородным:

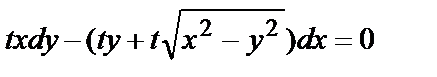
Разделив на t обе части уравнения, получаем данное уравнение.
Для решения этого однородного уравнения применим подстановку 


Сгруппируем слагаемые с  и с
и с 
 — уравнение с разделяющимися переменными. Умножив обе части на
— уравнение с разделяющимися переменными. Умножив обе части на  получим уравнение
получим уравнение  которое можно интегрировать.
которое можно интегрировать.

Подставив  получим общий интеграл данного Д.У.
получим общий интеграл данного Д.У.

Для выделения частного решения, удовлетворяющего данному начальному условию у=p при х=1, найдём значение произвольной постоянной С:  Отсюда С=1 и частный интеграл
Отсюда С=1 и частный интеграл 
Проверка: 

 ;
; 
По свойству пропорции
 или
или  — данное Д.У..
— данное Д.У..
Дата добавления: 2015-01-05; просмотров: 350; Мы поможем в написании вашей работы!; Нарушение авторских прав |